磁気モーメント（磁気双極子）とは｜定義・単位・性質と磁場との関係

磁気モーメント（磁気双極子）の定義・単位・性質と磁場との関係を図解でわかりやすく解説。電子から惑星までの例と数式で理解。

著者: Leandro Alegsa

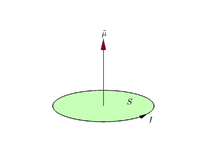
磁石の磁気モーメントとは、磁石が電流に与える力や、磁界が磁石に与えるトルクを決める量である。電流の輪、棒磁石、電子、分子、惑星などはすべて磁気モーメントを持っている。

磁気モーメントと磁界は、ともに大きさと方向を持つベクトルと考えてよい。磁気モーメントの方向は、磁石の南極から北極に向かっています。また、磁石から発生する磁界は、磁石の磁気モーメントに比例します。より正確には、磁気モーメントは通常、系の磁気双極子モーメントのことを指し、一般的な磁場の多極展開の第1項を生み出す。物体の磁場の双極子成分は、その磁気双極子モーメントの方向に対して対称であり、物体からの距離の逆3乗に比例して減少する。

定義と直感的な理解

簡単に言うと、磁気モーメントは「どれだけ強く、どの向きに磁場を作るか（あるいは磁場に反応するか）」を表すベクトル量です。たとえば、電流Iが流れる輪の面積をA（ベクトル面積）とすると、その磁気双極子モーメントは

μ = I · A（ベクトル）

で与えられます。向きは右手の法則によって決まり、電流の流れる向きに沿って親指を立てた方向がμの向きです。棒磁石の場合も同様に、磁石を北向きにする向きがμの方向（南極→北極）です。

単位と大きさの例

  • SI単位はアンペア・平方メートル（A·m2）。同じ次元でジュール毎テスラ（J/T）とも表される。
  • 電子一個の磁気モーメントの代表値はボーア磁子 μB = eħ / (2me) ≈ 9.274×10−24 J/T（量子力学的な単位）。
  • 地球の磁気双極子モーメントは約 7.9×1022 A·m2（規模の目安）。

磁場との関係（力・トルク・エネルギー）

  • トルク：外部磁場B中にある磁気モーメントμは、トルクτ = μ × B を受け、μがBの方向に整列するように回転する。
  • ポテンシャルエネルギー：U = −μ · B。磁場に対してμが整列するとエネルギーは低くなる。
  • 磁場分布（双極子場）：十分離れた点での磁場は双極子場に近似でき、SI単位系ではベクトル表現として B(r) = (μ0 / 4π) · [ (3 r (r · μ) − r^2 μ) / r^5 ] の形で与えられる。ここから分かるように、双極子成分は距離rの逆3乗（∝ 1/r^3）で減衰する。

原子・電子レベルでの起源

磁気モーメントの起源は主に二つに分けられる：

  • 荷電粒子の運動（軌道運動）に伴う循環電流
  • 粒子固有の量子性質としてのスピン磁気モーメント（電子スピンなど）

古典的には角運動量Lを持つ粒子は磁気モーメントμ = (q/2m) L を持つが、電子のような量子粒子ではスピンに対してg因子が関わり、実際の関係は μ = −g (e / 2m) S のようになる（電子は負電荷のため符号が負になる）。

物質としての磁気モーメントと磁化

多数の原子や分子が集まった物質では、単位体積当たりの磁気モーメントを磁化 M（単位 A/m）と呼ぶ。全体の磁気モーメントμ_totは磁化の体積積分で表される：

μ_tot = ∫ M dV

磁化は物質の常磁性・反磁性・強磁性など磁気的性質を決める重要な量であり、内部に束縛電流（境界面の面電流や体積の渦電流）を生じさせる。

測定法と応用

  • SQUID（超伝導量子干渉計）やホール磁気センサ、トルク磁力計などで微小な磁気モーメントを高感度に測定できる。
  • 磁気モーメントは磁気共鳴（NMR、ESR）や磁気データ記録、医療用MRI、地磁気の研究、磁気センサ応用など幅広い分野で重要である。

補足：多極展開との関係

物体の作る磁場を多極展開すると、最初の非自明な項が磁気双極子（磁気モーメント）である。高次の多極（四極子、八極子…）はより速く減衰し、遠方場では双極子項が支配的になる。

以上のように、磁気モーメントは小さな電子から大きな天体に至るまで「磁場を作る性質」や「磁場に反応する性質」を定量的に表す基本量であり、物理学・工学・天文学など多くの分野で中心的役割を果たす。

モーメントの2つの定義

教科書では、磁気モーメントの定義に2つの相補的なアプローチが用いられています。1930年代以前の教科書では、磁極を使って定義されていました。最近の教科書では、アンペリアン電流を用いて定義されています。

磁極の定義

物理学者は、物質中の磁気モーメントの発生源を「極」と表現する。北極と南極は、静電気の正と負の電荷になぞらえたものです。同じ大きさで極性が逆の磁極を持つ棒磁石を考えてみましょう。それぞれの磁極は磁力の源であり、距離が離れると磁力は弱まります。磁極は常にペアで存在するため、一方の磁極が引っ張ると他方の磁極が反発するため、磁極の力は部分的に相殺されます。この打ち消し合いは、磁極同士が接近しているとき、つまり棒磁石が短いときに最大となる。つまり、棒磁石が空間のある点で生み出す磁力は、極{\displaystyle p}の強さpと、極を隔てるベクトルlの2つの要素に依存する。{\displaystyle \mathbf {l} }の2つに依存する．瞬間は次のように定義される。

m = p l .{m = p mathbf {l} .となります。} {\displaystyle \mathbf {m} =p\mathbf {l} .}

南極から北極への方向を指している。磁気双極子は角運動量と関連しているので、電気双極子との類似性を取り過ぎるべきではない（「磁気モーメントと角運動量」参照）。とはいえ、磁極は、特に強磁性体への応用において、静磁場計算に非常に有用である。磁極アプローチを用いる実務者は、一般に磁場を回転しない磁場H {\\}で表す。}磁場を{\displaystyle \mathbf {H} }電場Eになぞらえて回転磁場Hで表現する。}{\displaystyle \mathbf {E} }.

電流ループの定義

平面的な閉ループに電流Iが流れI、ベクトル面積Sがあるとする。}{\displaystyle \mathbf {S} }( x {\displaystyle xx} , y {\displaystyle y}yこのベクトルの{\displaystyle z}座標は、ループをy z {\displaystyle yz}, z x {\displaystyle z}に投影したときの面積である。{\displaystyle yz}, z x { {displaystyle zx}に投影される領域である。{\displaystyle zx}およびx y {\\}{\displaystyle xy}面）に投影される領域である。その磁気モーメントm {\\bf {m}.}{\displaystyle \mathbf {m} }ベクトルは次のように定義される。

m = I S .{|S} 。} {\displaystyle \mathbf {m} =I\mathbf {S} .}

慣習的に、ベクトル領域の方向は、右手のグリップルール（手のひらがループの外縁に「触れている」ときに、右手の指をループの周りの電流の方向にカールさせ、親指をまっすぐにすると、ベクトル領域の方向、つまり磁気モーメントの方向を示す）によって与えられる。

ループが平面でない場合、モーメントは次のように与えられます。

m = I2 ∫ r × d r .{♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪♪\d}}\\mathbf {r} .} {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} .}

空間に任意の電流分布があるという最も一般的なケースでは、そのような分布の磁気モーメントは以下の式から求められる。

m 12= ∫r × J d V , {\\\\ ={frac {1}{2}}int ∫r\J}のタイムス\V,}を表しています。 {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,}

ここで，rは原点から体積要素の位置を指す位置ベクトル，Jは原点から体積要素の位置を指す位置ベクトルである．{\displaystyle \mathbf {r} }は原点から体積要素の位置を指す位置ベクトル、Jはその位置での電流密度ベクトルである。Jはその位置での電流密度ベクトル{\displaystyle \mathbf {J} }である。

上の式は、回転する荷電固体のような、移動する電荷の集合体の磁気モーメントを計算するために使用することができます。

J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} {\displaystyle \mathbf {J} =\rho \mathbf {v} ,}

ここで、ρ{\displaystyle \rho }はある点における電荷密度、v{\displaystyle \mathbf {v} }はその点の瞬間的な線速度である。

例えば、円周上を移動する電荷が生み出す磁気モーメントは

m = q12 r × v {displaystyle ˶‾᷄ -̫ ‾᷅˵} ={frac {1}{2}}\,q,\,r}。\v}}の{\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} },

ここで、rは円の中心に対する電荷qの位置であり、vは電荷の瞬間的な速度である。は円の中心qに対する電荷qの位置{\displaystyle \mathbf {r} }であり、vは電荷の瞬間的な速度で{\displaystyle \mathbf {v} }ある。

カレントループモデルを用いる実務者は、磁場をソレノイド磁場Bで表すのが一般的である。}{\displaystyle \mathbf {B} }静電場Dに相当するものである。}{\displaystyle \mathbf {D} }.

ソレノイドの磁気モーメント

上記の電流ループを一般化したものが、マルチターンコイル（ソレノイド）です。ソレノイドのモーメントは、個々のターンのモーメントのベクトル和である。ソレノイドがN個の{\displaystyle N}同一ターン（単層巻）を持つとする。

m = N I S .{|S} 。} {\displaystyle \mathbf {m} =NI\mathbf {S} .}

ソレノイドの3D画像。Zoom
ソレノイドの3D画像。

Zoom

モーメントm（moment m） {̶̶̶̶̶̶̶̶̶̶mは{\displaystyle \mathbf {m} }，面積S{\displaystyle S}，電流Iの平面電流ループであるI．

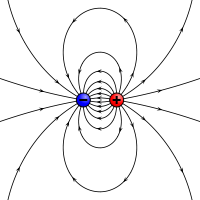
磁気モーメントの静電的類似性：有限の距離で隔てられた2つの対立する電荷。Zoom
磁気モーメントの静電的類似性：有限の距離で隔てられた2つの対立する電荷。

ユニット

磁気モーメントの単位は国際単位系(SI)の基本単位ではなく、複数の方法で表すことができる。例えば、電流ループの定義では、面積は平方メートル、IはIアンペアなので、磁気モーメントはアンペア平方メートル（A m）{\displaystyle {\text{A m}}^{2}}2で表される。また、モーメントのトルクの式では、トルクはニュートンメートル、磁場はテスラで表されるので、モーメントはテスラあたりのN.mで表されます（N.m T - {1displaystyle {text{N.m T}}^{-{\displaystyle {\text{N.m T}}^{-1}}1}}）。この2つの表現は等価である。

A m =2 N.m T - 。1{A m = N.m T}^{-1}．} {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}.}

CGSでは、電磁気学の単位にはいくつかの種類があり、主なものとしてESU、Gaussian、EMUがあります。これらのうち、CGSの磁気双極子モーメントの単位には、2つの代替（非等価）単位があります。

(ESU CGS) 1 statA-cm² = 3.33564095-14×10 (m2-A or N.m/T)

と（より頻繁に使用される）

(EMU CGSおよびGaussian-CGS）1erg/G = 1 abA-cm² = 10-3（m2-AまたはN.m/T）。

この2つの非等価なCGS単位の比（EMU/ESU）は、自由空間における光の速度にちょうど等しく、単位はcm/sで表されます。

本記事に掲載されている計算式は、SI単位ではすべて正しいですが、他の単位系では計算式の変更が必要な場合があります。例えば、SI単位では、電流I、面積Aの電流ループは、磁気モーメントI×A（下図参照）ですが、ガウス単位では、磁気モーメントはI×A/cとなります。

いくつかの素粒子の固有の磁気モーメントとスピン

粒子

SI単位の磁気双極子モーメント（10−27J/T）

スピン量子数（無次元）

エレクトロン

-9284.764

1/2

プロトン

14.106067

1/2

中性子

-9.66236

1/2

ミューオン

-44.904478

1/2

重陽子

4.3307346

1

トリトン

15.046094

1/2

磁気モーメントと磁化の関係については「磁化」を参照。

質問と回答

Q: 磁石の磁気モーメントとは何ですか?


A: 磁石の磁気モーメントは、磁石が電流に及ぼす力や磁場が磁石に及ぼすトルクを決定する量です。

Q: 磁気モーメントを持つ物体は?


A:電流の輪、棒磁石、電子、分子、惑星が磁気モーメントを持っています。

Q: 磁気モーメントと磁場の両方を考えるにはどうしたらよいですか?


A: 磁気モーメントも磁場も、大きさと方向を持つベクトルであると考えることができます。

Q: 磁石の磁気モーメントはどの方向を向いているのですか?


A:磁気モーメントの方向は、磁石の南極から北極に向かいます。

Q: 磁石の磁気モーメントと磁界の関係は?


A: 磁石が発生する磁場は、磁気モーメントに比例します。

Q: 通常、磁気モーメントとは何を指しているのですか?


A: 正確には、磁気モーメントとは、一般的な磁場の多極拡張の第一項を生成するシステムの磁気双極子モーメントのことを指します。

Q: 物体の磁場の双極子成分は、物体からの距離が離れるとどのように変化するのでしょうか?


A: 物体の磁場の双極子成分は、その磁気双極子モーメントの方向に対して対称であり、物体からの距離の逆3乗として減少します。


百科事典を検索する
AlegsaOnline.com - 2020 / 2025 - License CC3