数学の符号とは — 正負・無符号の定義と記号の意味

数学の符号（正負・無符号）の定義とプラス/マイナス等の記号の意味を図解でわかりやすく解説。初心者向けの入門ガイド。

数学では、符号という言葉は、正または負であるという性質を指します。すべての実数（0を除く）は正または負であり、したがって符号を持ちます。ゼロそのものは一般に「符号がない（無符号）」と扱われますが、文脈によっては「非負」や「非正」と表現されることがあります。実数に限らず、符号という言葉は数学全般で、数やベクトル、関数の値などの「正負を示す部分」を指すために使われます。通常、符号のない数字（先頭に + や − が書かれていない数値表記）は正の数と見なします。

正・負・無符号の定義と性質

正の数：数 x が x > 0 を満たすとき「正」であり、通常は先頭に + を付けることもできます（例：+3）。
負の数：数 x が x < 0 を満たすとき「負」であり、先頭に − を付けて表します（例：−5）。
無符号（符号なし）：ゼロは正でも負でもないため「無符号」とされます。ただし、解析や不等式の議論では「非負（≥0）」や「非正（≤0）」と表現することが多い点に注意してください。

符号を表す記号と用法

符号を示す記号にはいくつか種類があります。

• 単項の +, −：数の先頭に付いてその数が正か負かを示します。省略された場合は正と見なします。
• ±（プラスマイナス）：二つの符号の両方を表すときに用いられます。方程式の解や公差の範囲などで「a ± b」は「a + b」および「a − b」の両方を意味します。
• ∓：± と組で使われ、上下の符号を逆にする際に用いられます（例えば、a ± b と a ∓ b の組合せ）。
• 乗算記号など他の記号：文脈によっては、記号一般を「sign」と呼ぶことがありますが、数学では通常「符号」は正負に関する意味で使われます。

符号関数（sgn）と絶対値との関係

符号を関数として表すときは符号関数（符号判定関数）sgn を使います。実数 x に対して

sgn(x) = 1 （x > 0）、 0 （x = 0）、 −1 （x < 0）

が成り立ち、任意の実数 x に対して次の関係が便利です：
x = sgn(x) · |x|。ここで |x| は絶対値で、数の大きさ（符号を除いた値）を表します。

その他の注意点・応用

• 複素数には「正」「負」という自然な順序がないため、実数で使うような意味での符号は通常定義しません。複素数については偏角（argument）や実部・虚部の符号で性質を議論します。
• 計算機科学では「有符号整数（signed）」と「無符号整数（unsigned）」という区別があります。これはビット表現における解釈の違いで、数学での「符号」とは文脈が異なりますが、日常的に「符号付き／符号なし」と呼ばれます。
• 方程式の解集合などで ± を使う場合は、個々の符号ごとに別々の式として扱うことが多いので注意してください（例：x = ±√a は x = √a または x = −√a の二つの解を示す）。

まとめると、数学における「符号」は主に「正（+）・負（−）・無符号（0）」を示す概念であり、記号としては単項の +/−、複合的には ±/∓、関数的には sgn が使われます。文脈によっては記号一般を指して「sign」と言うこともありますが、意味するところはその場に依存します。

符号の意味

ゼロは正でも負でもないので、未知数の符号を指すときに次のように使われることがあります。

• 数は0より大きければ正の数である。
• 数値が0より小さいと負になります。
• 数は0以上の場合、非負である。
• ゼロ以下であれば非正数である。

したがって、非負の数は正またはゼロであり、非正の数は負またはゼロである。例えば、実数の絶対値は常に非負であるが、必ずしも正ではない。

実数や整数の値を取る関数にも同じ定義が使われることがある。例えば、ある関数の値がすべて正であれば正関数、すべての値が非負であれば非負関数と呼ばれる。

角の符号

多くのテキストで、角、特に位置する角や回転角の測定値とともに符号が表示されることがよくある。このような場合、記号はその角度が時計回りか反時計回りかを示している。様々な表記方法があるが、数学では反時計回りの角度を正、時計回りの角度を負と数えるのが一般的である。

また、回転軸の向きが決まっていれば、3次元の回転角度に符号を付けることも可能である。具体的には、通常、軸の周りを右回りに回転すると正となり、左回りに回転すると負となる。

方位記号

算数や物理の世界では、ある方向をプラス、マイナスと表記することが一般的である。基本的な例として、数直線は通常、右に正の数、左に負の数が描かれる。

直交平面上では、通常、右向きと上向きを正として考え、右向きを正のX方向、上向きを正のY方向とする。

その他の意味

実数の符号のほか、符号という言葉は数学や科学の世界では様々な関連した使われ方をしている。

• グラフ理論において、符号付きグラフとは、各辺に正負の符号を付けたグラフのことである。
• 物理学では、電荷には正負の符号がつく。一般に、陽子と同じ符号の電荷を正電荷といい、電子と同じ符号の電荷を負電荷という。

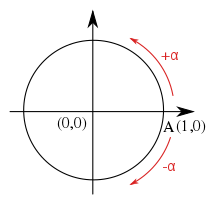
X軸から測ると、単位円上の角度は反時計回りが正、時計回りが負となる。


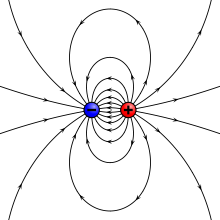
電荷にはプラスとマイナスがあります。

文字で検索