カオス理論
カオス理論は数学の一分野です。この理論は、非常に敏感なシステムを対象としています。ほんの少しの変化で、システムの挙動がまったく変わってしまうのです。
カオス系のスタート位置のごくわずかな変化が、しばらくすると大きな変化をもたらす。大型コンピュータでも数日以上先の天気が分からないのはこのためだ。たとえ完璧に計測された天気であっても、ちょっとした変化や誤差で予測は完全に狂ってしまう。蝶でさえ天候を変えるほどの風を起こすことができるので、カオスなシステムを「バタフライ効果」と呼ぶこともある。小さな風がどのように天気を変えるのか、それを教えてくれるほどのコンピュータはない。
天候のように、一見するとランダムに見えるシステムもありますが、カオス理論では、このようなシステムやパターンはそうではないかもしれないとしています。実際に起こっていることに十分注意を払えば、カオス的なパターンに気づくかもしれません。
カオス理論の主な考え方は、プロセスの開始時のわずかな違いが、時間の経過とともにプロセスに大きな変化をもたらすというものである。量子カオス理論は、カオス理論の研究における新しいアイデアです。量子物理学を扱っています。
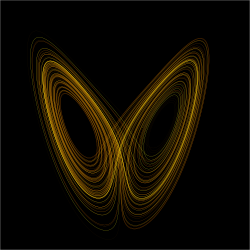
ローレンツアトラクターと呼ばれるカオス関数のグラフ。
この2つのつながった振り子が少しでも違う位置からスタートすると、グレーのラインは全く違うものになります。
例
例えば、ある地点に取り付けられた振り子が自由に揺れているとします。1つ目の振り子に2つ目の振り子を接続すると、システムは全く違ったものになります。全く同じ位置からスタートすることは非常に難しく、目に見えないほど小さなスタート位置の変化でも、振り子の揺れはすぐに以前とは違ったものになってしまいます。
カオス理論の研究で非常に重要なのは、フラクタルと呼ばれる数学の関数の研究です。フラクタル関数は、カオスシステムのような働きをします。開始値を少し変えるだけで、関数の値がランダムに変化します。フラクタル関数は数学的であるため、研究しやすいのが特徴です。
関連ページ
- 不連続関数
質問と回答
Q:カオス理論とは何ですか?
A:カオス理論とは、非常に繊細で、システムのちょっとした変化で全く違う動きをするシステムを研究する数学の一分野です。
Q:なぜ大型コンピュータでも正確な天気予報ができないのか?
A:大型コンピュータでも天気予報に失敗するのは、天気のようなカオスシステムの開始位置は小さな変化に非常に敏感で、小さな誤差や変化でも予報が完全に間違ってしまうからです。
Q:「バタフライ効果」とは何ですか?
A: 「バタフライ効果」とは、カオス理論の概念の一つで、蝶の羽ばたきのような小さな変化でも、気象などのカオス系に大きな影響を与えるという考え方です。
Q: ランダムに見えても、実はそうでないシステムもあるのでしょうか?
A:はい、カオス理論では、最初はランダムに見えても、実はそうではないシステムやパターンがあり、注意深く観察することでカオスパターンを明らかにすることができると考えられています。
Q: カオス理論の主な考え方は何ですか?
A: カオス理論の主な考え方は、プロセスの開始位置のわずかな違いが、時間の経過とともにプロセスに大きな変化を与えるというものです。
Q: 量子カオス理論とは何ですか?
A: 量子カオス理論とは、カオス理論の研究において、その原理を量子物理学に応用した新しい考え方です。
Q:非常に小さな変化はカオス系にどのような影響を与えるのですか?
A: カオスシステムの開始位置のごく小さな変化が、時間の経過とともにその挙動に大きな違いをもたらすことがあります。これは、カオス系が非常に敏感であり、小さな変化がその挙動に大きな違いをもたらすからです。
