グラフ（関数）とは｜定義・直交座標と軸の役割
グラフとは、2つ以上の量や変数のつながり（関係）を視覚的に表現した図のことです。右のグラフを見てください。数値や測定値の対応関係を一目でとらえやすくするため、観察や解析、予測に広く使われます。
直交座標系と軸の役割
もっともよく使われるグラフの形式は、長方形の格子状に表した直交座標系（デカルト座標系）です。ここでは2本の直角に交わる線（軸、axisの複数形）が基本になります。
- 一方は上向きの縦軸（通常はy軸）で、もう一方は右向きの水平軸（通常はx軸）です。
- 軸の交点は原点（origin）と呼ばれ、通常は座標 (0, 0) を表します。図では左下隅で交わることもありますが、原点は図の中央や任意の位置に置くことができます。
- 各軸には長さ方向に目盛り（tick marks）があり、これにより数値を読み取ります。目盛りは紙の上の定規に相当し、各測定値は軸に沿った対応する目盛りの位置で示されます。
点のプロットと関数のグラフ
点をプロットする基本は、各データ点を座標 (x, y) の位置に対応させることです。例えば点 (3, 2) は、x軸で3の位置、y軸で2の位置が交わる場所に置かれます。関数 y = f(x) のグラフは、その関数を満たすすべての点 (x, f(x)) をプロットして得られる曲線（または直線）です。
- 連続的な関数は滑らかな曲線として現れます（例：二次関数や三角関数）。
- 離散データは点で示され、必要に応じて点間を線で結んで変化の傾向を表します。
- 直線の傾き（slope）や切片（intercept）は関係の強さや基準値を示す重要な指標です。
目盛りと尺度（スケール）の重要性
グラフを正しく読み解くには、各軸の目盛りや単位、スケールの設定が重要です。目盛りの間隔が等しい等間隔スケールを使うことで、角度や傾きの比較が直感的になりますが、対数スケールなど特別なスケールを使う場合もあります。必ず軸にラベル（変数名と単位）を付け、必要なら凡例やタイトルを付けて何を表しているかを明示します。
グリッド線、ラベル、凡例
格子（グリッド）線は目盛りを読みやすくし、点や曲線の位置を正確に把握するのに役立ちます。グラフには次の要素を加えると実用性が高まります。
- タイトル：グラフ全体の主題を示す
- 軸ラベル：x軸・y軸の変数名と単位を明記
- 凡例（レジェンド）：複数のデータ系列がある場合に各系列を識別
- 注釈：重要な点や外れ値、データの出所を示す
チャート・ダイアグラムとの違い
グラフは、特に数値の対応関係や関数の形を示すチャートやダイアグラムの一種です。一般に、「チャート」や「ダイアグラム」は幅広い図表を指し、必ずしも量と量の数値的関係を示すとは限りません。たとえば、フローチャートや樹形図は手続きや階層構造を示す図で、数値の対応を直接表すグラフとは用途が異なります。
グラフを使う際のポイント
- データの性質（連続か離散か、スケールの適切さ）を考えてグラフ形式を選ぶ。
- 軸の範囲やスケールを誤ると誤解を招くため注意する。
- ラベルや単位を明示し、凡例や注釈で読み手の理解を助ける。
- 目的（比較、傾向の把握、関数の解析など）に応じて折れ線、散布図、ヒストグラムなど適切な図を選ぶ。
このように、グラフは数値や関数の関係を視覚的に表現する強力なツールであり、正しい作り方と読み方を知ることで情報を正確に伝え、理解を深めることができます。
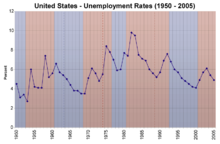
このグラフは、米国における年ごとの失業率を示したものです。
簡単なグラフの描き方
例えば、自分の成長過程の身長をグラフにしたいとします。縦軸に身長（cm）、横軸に年齢（年）をとってみましょう。
例えば、1歳の時の身長が60cm、2歳の時の身長が85cm、3歳の時の身長が95cmだったとします。縦軸に身長50cmのマークを通る想像上の直線を引きます。そして、横軸には1歳を通る想像上の直線を引きます。その2本の線が交わるところに点を描きます。実際には、想像線はグラフ用紙に置き換えられています（下図参照）。この交点を描くことを「1歳の50cmという点をプロットする」と言います。
そして、2年目は85センチ、3年目は95センチとプロットしていきます。さらに多くの年の高さがあれば、4年目、5年目、とプロットしていきます。グラフ上に十分な点があれば、プロットした各点を通る線を引き、グラフを折れ線グラフにすることができます。例えば、右上の折れ線グラフは、縦軸に失業率（％）、横軸に年（1950年から2005年まで）をとったものです。
例えば、自分の身長と弟の身長の両方を1つのグラフにしたいとします。これは、2組のプロットされた点として表現することができます：1つはあなたの、もう1つはあなたの兄弟のものです。あなたのプロットとお兄さんのプロットを見分けるために、異なる色を使うことができます。また、上の失業率のグラフの同じ年に対して、国内総生産（10億ドル）を2本目の線でプロットすることもできます。そうすれば、GDPと失業率の関係がわかります。
グラフの用途
グラフは情報を見やすくします。これは、2つ以上の数字が何らかの形で関連している場合に特に当てはまります。
例えば、冒頭の失業率のグラフは、表の形で表現することができます。こんな感じで。
| 年 | 失業率 |
| 1950 | 4.5% |
| 1951 | 3.1% |
| 1952 | 3.4% |
| などです。 |
しかし、長い数字の羅列では、その意味がわかりにくい。そこで、表をグラフにして表現すると、よりわかりやすくなります。特に、2つのデータの関係性がわかりやすくなります。例えば、グラフを見ると、60年代後半の失業率は比較的低く、80年代前半の失業率は比較的高いことが一目瞭然です。
科学者やエンジニアは、データの大まかな意味や重要性をよりよく理解するためにグラフを使用します。セールスマンやビジネスマンは、セールスやビジネスのプレゼンテーションにおいて、自分の主張に重要性を持たせるためにグラフを使用します。多くの点がプロットされたグラフは、手書きではなくコンピュータで作成されることもある。
数学者は、測定しなくても「自分で描いた」グラフを使う。例えば、x＝yという式は、xの値とyの値が常に等しいということを表しています。この式を、xを横軸、yを縦軸としたグラフにすると、正確に45度の角度を持った直線のようなグラフになります。このようなグラフを用いた数学を解析幾何学といいます。
グラフ用紙
通常、グラフは方眼紙と呼ばれる特別にデザインされた紙で作成されます。この紙には、縦横の線が均等に描かれている。右は方眼紙の一例。
グラフの種類によって、必要なグラフ用紙の形が異なります。上の記事でお話ししてきたのは、最も一般的なグラフと方眼紙の形です。直方体グラフやデカルトグラフと呼ばれるものです。しかし、グラフ用紙に均等に描かれている縦線や横線は、グラフそのものではなく、グラフ用紙の一部です。グラフとは、プロットされた点の集合であり、その軸でもあります。
グラフ（および方眼紙）には、直交座標以外にも様々な種類があります。棒グラフ、円グラフ、極軸グラフ、散布図、立体図、対数図などがあります。
直方体のグラフ用紙
質問と回答
Q: グラフとは何ですか?
A: グラフとは、言葉、特に2つ以上の量のつながりを表現するために作られた絵です。
Q: 2つの数値または測定値の関係は、単純なグラフでどのように示されますか?
A:2つの数値や測定値の関係は、グリッドの形で表示されます。
Q: 直交座標系とは何ですか?
A: 直交座標系とは、2つの測定値が互いに直角の2つの異なる線に配置された長方形のグラフのことです。
Q: 直方体のグラフの縦軸と横軸はどのように配置されていますか?
A:縦軸は上へ、横軸は右へ進みます。
Q:長方形のグラフで、線と軸はどこで交わるのですか?
A:グラフの左下で線と軸が合流します。
Q: グラフの目盛りは何ですか?
A:ティックマークは、各軸に沿ったマークで、各測定値を示すために紙に描かれた定規のような役割を果たします。
Q:グラフと図表の違いは何ですか?
A:グラフはある量と他の量を関連付けますが、図表はそうでない場合があります。フローチャートや樹形図は、グラフではない図表の例です。
