3D

3D（または3-D）とは、3次元、または3次元を持つことを意味します。例えば、箱は立体的で、紙のように薄いものではなく、しっかりしています。箱にはボリュームがあり、上下、左右（側面）、正面と背面があります。箱を裏返して別の面（面、面、単純に側面と呼ぶ）から見ることができます。

寸法は、インチ、ミクロン、マイル、キロメートル、またはその他の長さの単位で測定可能です。

三次元は、長さ（または奥行き）、幅（または幅）、高さと呼ばれることが多い。目的によっては別の言葉を使うこともあります。

3Dグラフィックスは、ビデオゲームやアニメーション映画を作るために使用されます。画像を画面上で立体的に見せるためには、多くの計算が必要です。現代のコンピュータは通常、これらの計算を処理するためにGPU（Graphics Processing Unit）を搭載しています。

両眼視は第三次元を見やすくします。

3Dボックス

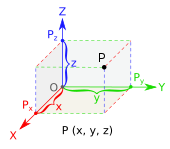
X軸」「Y軸」「Z軸」の写真。

幅、高さ、長さを測る線で構成された3Dの数学的な絵、またはグラフ。

数学では

直交座標系では、長さ、幅、高さは、書きやすいように、あるいは値がわからない場合には、文字（変数）で与えられます。多くの場合、Xは幅、Yは高さ、Zは長さである。他にも球面座標などの3次元座標系には、直線的な測定値と角度的な測定値の両方があります。

三次元の形状や寸法を数学的に研究することをソリッドジオメトリといいます。

時間を第四の次元と見る人もいます。また、測定されています。秒、時間、年などの時間の単位で測定されます。

A: 3Dとは3次元、3つの次元を持つという意味です。

A: 箱は三次元で、立体で、体積があります。また、上下、左右（側面）、前後があります。

A: 3つの次元は、しばしば長さ（または奥行き）、幅（または幅）、高さと呼ばれます。

A: 3Dグラフィックスは、ビデオゲームやアニメーション映画の制作に使用されます。

A: 最新のコンピュータには、通常、これらの計算を処理するためのGPU（グラフィック・プロセッシング・ユニット）が搭載されています。

A:両眼視機能により、3次元を簡単に見ることができます。

A: 画面上で絵を立体的に見せるためには、多くの計算が必要です。