重力加速度（g）とは：定義・単位・地球表面での値と変動要因

重力加速度（g）の定義・単位（m/s²）、地球表面での標準値9.80665や地点別の変動要因をわかりやすく解説。

著者: Leandro Alegsa

重力によって物体が受ける加速度を重力加速度という。SI 単位は m/s2 です。重力加速度はベクトルであり、大きさと方向の両方を持つことを意味する。地球表面での重力加速度は g という文字で表され、9.80665 m/s2 (32.1740 ft/s2 ) という標準的な値が定義されています。しかし、自由落下中の物体の実際の加速度は、場所によって異なります。

定義と単位

重力加速度（g）は、天体（ここでは地球）が物体に及ぼす引力によって生じる加速度です。SI単位は m/s2 で、地球物理学では Gal（ガル） という単位も使われ、1 Gal = 1 cm/s2 = 0.01 m/s2 です。

理論的な式

点質量による単純化した万有引力から求めると、半径 r の地点での重力加速度は

g(r) = GM / r2（G：万有引力定数、M：天体の質量）で与えられます。地球の場合、地表近傍では半径 r = R + h（R：地球の平均半径、h：高度）と近似でき、h が小さいときはテイラー展開により

g(h) ≈ g0 (1 - 2h / R) と近似されます。これより、地表近傍では高度が 1 m 増すごとに g は約 3.08 × 10−6 m/s2 減少し、1 km では約 0.00308 m/s2（約 0.308 mGal）減少します。

地球表面での標準値と緯度依存性

  • 国際的に定義された標準重力：g0 = 9.80665 m/s2（定義値）。
  • 実際の地球表面での g は緯度によって変わり、赤道付近で最低（約 9.7803 m/s2）、極付近で最大（約 9.8322 m/s2）になります。これは地球が完全な球体ではなく回転楕円体（扁球）であることや、地球自転に伴う遠心力の影響によるものです。
  • 自転による遠心力の大きさは赤道で約 0.034 m/s2 に相当し、これが見かけの重力を低下させる主因の一つです。

地球上での変動要因

同じ緯度・高度でも局所的に g が変化する理由は複数あります：

  • 高度：前述のように高さが増すと重力は減少します。
  • 緯度と自転：遠心力や地球の扁平による効果で緯度依存性があります。
  • 地質的要因：地殻やマントル内の密度異常（高密度の岩体や空洞など）により局所的に増減します。これを利用して資源探査や地殻構造の推定が行われます。
  • 潮汐効果：月や太陽による潮汐力が地球の形状や重力場に微小な変化を与えます（時間変動）。
  • 大気や浮力：大気圧や気温の変化による密度変化がわずかに影響します。

測定方法と精度

  • 相対測定：重力差を比較する 相対重力計（ばねや傾斜式）で観測し、地形や地下密度の変化を調べます。
  • 絶対測定：物体の自由落下時間を精密に測る、またはレーザー干渉計・原子干渉計を用いる 絶対重力計 により 1 μGal（10−8 m/s2）程度の高精度で測定可能な装置もあります。

実用上の留意点と応用

  • 工学や計量の分野では、重力のわずかな違いが秤や加速度計の校正に影響するため、場所ごとの g を考慮することがあります。
  • 地球物理学や地質探査では、重力測定から地下の密度構造を推定して鉱床探査や地殻変動の把握に利用します。
  • 精密実験（例えば物理定数の測定や慣性センサーの校正）では、基準となる g0 = 9.80665 m/s2 と現地の重力との差を補正して扱います。

まとめると、重力加速度 g は定義上は一定の「標準値」があるものの、地球上の実際の値は緯度・高度・地質・時間変動など多くの要因でわずかに変わります。高精度を要する場面ではこれらの変化を測定・補正することが重要です。

重い物体が軽い物体より速く落ちない理由

アイザック・ニュートンは，結果力が質量に加速度を掛けたものに等しいことを見出したが，記号では F = m a {displaystyle F=ma}{\displaystyle F=ma} .これは a = F m {displaystyle a={hatfrac {F}{m}} } } となるように再整理することができる．{\displaystyle a={\frac {F}{m}}\ }.落下する物体の質量が大きければ大きいほど、それを地球に向かって引っ張る重力は大きくなる。上の式では、これはF { {displaystyle F}F .しかし、力が大きくなったり小さくなったりするのは、質量が大きくなったり小さくなったりする回数と同じで、その比率は一定である。どのような状況でも、F m {displaystyle {disrac {F}{m}} }{\displaystyle {\frac {F}{m}}\ } はキャンセルされ、9.8m/s程度の一様な加速度となる2 .これは、質量に関係なく、すべての自由落下物体が同じ速度で加速することを意味する。

次のような例を考えてみましょう。

a = 49 N 5 k g = 9.8 N / k g = 9.8 m / s 2 {displaystyle a={frac {49,\mathrm} N}{5,\mathrm {kg}}} =9.8,\mathrm {N/kg} =9.8,\mathrm {m/s^{2}} となります。} {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }

a = 147 N 15 k g = 9.8 N / k g = 9.8 m / s 2 {displaystyle a={frac {147,\mathrm} N}{15,\mathrm {kg}}} =9.8,\mathrm {N/kg} =9.8,\mathrm {m/s^{2}} となります。} {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} }

表面加速度

場所にもよりますが、地表の物体は 9.76 ～ 9.83 m/s2 (32.0 ～ 32.3 ft/s2 ) の加速度で落下します。

地球は正確な球体ではありません。赤道付近の半径が極付近の半径よりもわずかに大きい、「つぶれた」球体に近いのです。このため、極地では重力加速度がわずかに大きくなり（地球の中心に近く、重力は距離に依存するため）、赤道では重力加速度がわずかに小さくなるという効果がある。また、求心加速度があるため、赤道では極点よりも重力による加速度がわずかに小さくなります。地中の岩石の密度が変化したり、近くに山があったりすると、重力加速度にわずかな影響を与えることがあります。

高度

物体の加速度は、高度によって変化します。地球の中心からの距離による重力加速度の変化は、逆二乗の法則に従います。つまり、重力加速度は地球の中心からの距離の2乗に反比例します。距離が2倍になると重力加速度は4分の1になり、3倍になると重力加速度は9分の1になるというように、重力加速度が変化します。

重力加速度 ∝ 1 distance 2 {displaystyle {} {}mbox{gravitational acceleration}} \propto {}frac {1}{distance}^{2}} }. {\displaystyle {\mbox{gravitational acceleration}}\ \propto \ {\frac {1}{{\mbox{distance}}^{2}}}\ }

重力加速度 × 距離 2 = k {displaystyle {} \times {{mbox{distance}}^{2}} ={k}}. {\displaystyle {\mbox{gravitational acceleration}}\ \times {{\mbox{distance}}^{2}}\ ={k}}

地球の表面では、重力による加速度はおよそ9.8 m/s2 (32 ft/s2 )です。地球の中心までの平均距離は、6,371 kmです。

k = 9.8 × 6371 2 { {displaystyle {k}={{mbox{9.8}}}} \times {{mbox{6371}}^{2}}}. {\displaystyle {k}={\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}

定数k { {displaystyle k} を使ってkを使うと、ある高度での重力加速度を計算することができます。

重力加速度 = k distance 2 {displaystyle {} {} {gravitational acceleration}} ={}frac {k}{}{}mbox{distance}^{2}} } }. {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {k}{{\mbox{distance}}^{2}}}\ }

例題地表から1,000km上空での重力加速度を求めなさい。

6371＋1000＝7371 {\displaystyle 6371+1000=7371}

∴ 地球の中心からの距離は7,371km。

重力加速度 = 9.8 × 6371 2 7371 2 ≒ 7.3 {displaystyle {mbox{gravitational acceleration}} ={frac {{mbox{9.8}} ³times {{mbox{6371}^{2}}} {{mbox{7371}^{2}}}} ╱ 7.3｝ {\displaystyle {\mbox{gravitational acceleration}}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}^{2}}}{{\mbox{7371}}^{2}}}\ \approx 7.3}

∴ 地表から1,000km上空での重力による加速度は7.3m/s2 (24 ft/s2 ) です。

高度100kmにある地球大気と宇宙空間の境界線である「カールマンライン」の重力加速度は、海面より約3％低いだけである。

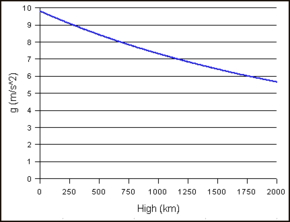
物体の高さに伴う重力加速度の変化Zoom
物体の高さに伴う重力加速度の変化

質問と回答

Q: 重力加速度とは何ですか。
A:重力加速度とは、重力によって物体が得る加速度のことです。

Q:重力加速度のSI単位は何ですか?


A:重力加速度のSI単位はm/s2です。

Q: 重力加速度はスカラーですか、それともベクトルですか?


A: 重力加速度は、大きさと方向の両方を持っているので、ベクトルです。

Q: 地表の重力加速度を表す記号は何ですか?


A: 地表の重力加速度を表す記号は g です。

Q: 地表の重力加速度の標準値は?


A: 地表の重力加速度の標準値は、9.80665 m/s2 (32.1740 ft/s2)です。

Q: 自由落下中の物体の実際の加速度は、場所によって異なりますか?


A: はい、自由落下中の物体の実際の加速度は場所によって異なります。

Q: 重力加速度の定義は何ですか?


A:重力加速度とは、重力によって物体が得る加速度のことで、地球表面での標準値は9.80665m/s2で、gで表されます。


百科事典を検索する
AlegsaOnline.com - 2020 / 2025 - License CC3