分子振動とは:定義とメカニズム、代表例(H2・N2・O2)
分子振動の定義とメカニズムを図解でわかりやすく解説。H2・N2・O2の代表例で基礎からスペクトル応用まで学べる入門ガイド
分子振動は、並進運動(分子全体が同じ方向に進むこと)、回転運動(分子がこまのように回ること)と並ぶ3種類の分子の運動の一つです。分子振動とは、分子内の原子と原子の結合距離や角度が時間とともに周期的に変化する運動を指します。原子を質量のある球、化学結合をバネと考える「質量-ばねモデル」で直感的に理解できます。最も単純な振動は2つの原子間で起こる「伸縮(ストレッチ)」で、これが分子振動の基本的な例です(ここでは「振動の最も単純な例」と言えます)。
基本的なメカニズム
- 振動は平衡位置の周りで行われ、ばねに相当する力の定数(力定数 k)と原子の効果的質量(縮約質量 μ)によって振動角周波数 ω が決まります。古典的には ω = √(k/μ) で近似されます。
- 量子力学的には振動エネルギーは離散(量子化)され、簡単な調和振動子近似ではエネルギー準位は E_v = (v + 1/2)hν(v = 0,1,2,...)となり、基底状態でもゼロ点エネルギー(1/2 hν)を持ちます。
- 多原子分子では、全体として3N(Nは原子数)の運動自由度のうち平行移動(3)と回転(線形分子は2、非線形分子は3)を除いた残りが振動モード(正準モード)になります。各モードは伸縮(ストレッチ)や曲げ(ベンド)などに分類されます。
分光学的な性質(IRとラマン)
- 赤外(IR)吸収は、分子振動が分子の双極子モーメントを時間的に変化させる場合に観測されます。したがって、双極子の変化がない振動はIRでは活性になりません。
- 一方、ラマン散乱は分子の分極率の変化に敏感で、IRで見えない振動がラマンで観測されることがあります。
- 例として、同種原子からなる二原子分子(同原子分子)は振動によって双極子モーメントが変化しないためIR不活性ですが、ラマン活性です。
代表例:二原子分子(H2, N2, O2)
このような単純な分子の例としては、水素 H2、窒素 N2、酸素 O2 などがあります。これら二原子分子は、1本の結合に対する単一の伸縮振動モードを持ちます。特徴は次の通りです。
- 振動数は結合の強さ(力定数 k)と縮約質量 μ に依存します。質量が小さく結合が強いほど振動数は高くなります(たとえばH2は非常に高い振動周波数を持ちます)。
- H2, N2, O2はいずれも同原子分子であり、振動による双極子変化がないため常温常圧下の赤外吸収は基本的に見られません(IR不活性)。しかし、ラマン分光では観測可能です。
- 実測される振動遷移は赤外領域に対応することが多く、分子の振動スペクトルは化学結合の情報(結合次数、極性、周囲の化学環境)を反映します。
応用と視覚化のヒント
- 分子振動の理解は、赤外吸収スペクトルやラマンスペクトルの解析、化学結合の強さ評価、反応経路の解析(遷移状態の振動モード)などに不可欠です。
- 視覚的には、分子モデルで原子を小球、結合をバネで表し、平衡位置からのゆっくりとした往復運動を想像すると分かりやすいです。多原子分子では各原子が協調して動く「正準振動モード」をアニメーションで見ると直感的に理解できます。
まとめ: 分子振動は原子間の相対運動であり、力定数と縮約質量で決まる周期運動です。スペクトル解析(IR、ラマン)を通じて分子構造や結合性を調べる重要な手法です。
振動の種類
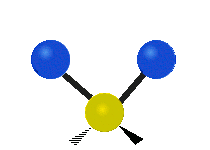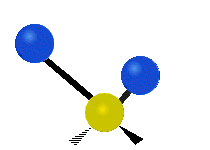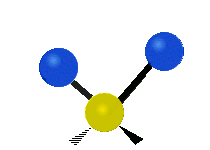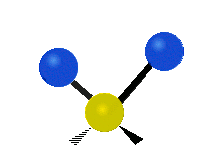
もし分子が2つ以上の原子を持つ場合、事態はさらに複雑になる。例えば、もう1つだけ原子を追加して、水H2 Oのように3つの原子を持つようになったとします。ここでは、2つの水素原子がともに中心の酸素原子に結合しています。水素の場合は1種類の伸縮振動でしたが、水の場合は2種類の伸縮振動と、下に示すような4種類の屈曲振動と呼ばれる振動があることを覚えておいてください。
CH2 グループや水のような分子の原子は、対称的および反対称的な伸縮、はさみ打ち、揺れ、揺れ、ねじれの6種類の振動をすることができます。
| シンメトリカルストレッチング | 反対称性ストレッチ | シザリング |
|
|
|
|
| ロッキング | ワギングの様子 | ツイスト |
|
|
|
|
対称伸縮:結合している2つの原子が同時に中心原子から離れる方向と中心原子へ向かう方向に動く場合。
反対称伸縮:くっついた2つの原子が同時に中心原子から離れず、中心原子に向かって移動する場合。
シザリングシザリングとは、その名の通り、2つの原子が互いに遠ざかったり近づいたりすることである
ロッキングこの運動は、時計の振り子が行ったり来たりするのに似ていますが、ここでは原子が振り子となり、1つではなく2つになっています。
wagging:手を前に出し、2本の指を「V」の字に曲げ、手首を曲げたり離したりする。このとき、指の先が付属原子、手首が中心原子となる。
を捻る。この運動は、人がトレッドミルの上を歩いているようなもので、腰が中心原子で、足が2つの付属原子である。
3個以上の原子を持つ分子
原子が3つ以上ある分子はさらに複雑で、「振動モード」と呼ばれることもある振動をさらに多く持っている。新しい振動モードは、基本的に上に示した6つの組み合わせのそれぞれで構成されている。分子内の原子の数が多ければ多いほど、より多くの組み合わせが可能になる。N個の原子を持つほとんどの分子では、その分子で可能な振動の数は3N - 6である。一方、直線状の分子(原子が直線状に並んでいる分子)では、3N-5の振動モードがある。
エネルギーと振動の関係
ニュートン力学
ニュートン力学では、結合をバネのように扱うことで、分子の振動を計算することができる。これは、バネのように、結合を伸ばすにはエネルギーが必要で、また、結合を絞るにもエネルギーが必要であることから、有用である。結合を伸ばしたり縮めたりするのに必要なエネルギーは、ばね定数kで表される結合の硬さと、μで示される両端に付着した2つの原子の還元質量、つまり「質量中心」に依存する。結合に振動を与えるために必要なエネルギーを表す式は次の通りです。
E = h ν = h 2 π k μ .Ȃ E=h Ȃnu ={h Ȃover {2pi }}{sqrt {k Ȃover {mu }}.Ȃ!}
h: はプランク定数
ν:周波数であり、結合が押し縮められ、再び引き離される速度を表す。νが大きいほど、この速度は速くなる。
Ε:結合を押したり引いたりするのに必要なエネルギーです。
μ:還元質量は、原子の2つの質量を掛け合わせ、その足し算で割ったものです。
μ = m 1 m 2 m 1 + m 2 .{displaystyle \mu ={m_{1}m_{2}} .\m_{1}+m_{2}}.\!}
量子力学
量子力学では、ある特定のエネルギー(エネルギー準位)のみが許されることを除けば、ニュートン力学と全く同じ式でバネを記述することができる。エネルギーレベルは、人が一度に一段ずつしか昇り降りできない梯子の段のようなものだと考えてください。その人は段と段の間に立つことができないので、結合はエネルギーレベル間のエネルギーを持つことができないのです。この新しい数式はこうなる。
E n = h ν = h ( n + 1 2 ) 1 2 π k m {displaystyle E_{n}=h\nu =h\left(n+{1 \over 2}right){1 \over {2pi }}{centaqrt {k \over m}} {!}
ここで、n は量子数または「エネルギー準位」であり、0, 1, 2 ... の値をとることができる。エネルギーレベルは一度に1レベルしか上がらないか下がらないという声明は、エネルギーレベル間の遷移のみが許されるという選択則として知られています。
Δ n = ± 1 {displaystyle \Delta n=pm 1}.
ここで、 \Delta n はエネルギー遷移である。
振動運動の応用
ある周波数の光が、その周波数に対応する振動を持つ分子に当たると、その光が分子に吸収され、光のエネルギーによって結合がその振動運動で動くのです。吸収された光を調べることで、ある種の分子結合があるかどうかがわかり、その結合を持つ分子のリストと照合することができるのです。
しかし、ヘリウムやアルゴンのように、原子が1つしかなく、結合を持たない分子もあります。つまり、複数の原子を持つ分子と同じように、光を吸収することができないのです。
分子振動を利用する化学の具体的な分野としては、赤外分光法(IR)とラマン分光法(Raman)があり、IRの方が広く利用されており、それ自体3つのサブフィールドを持っています。これらのサブフィールドは、Near IR、Mid IR、Far IR spectroscopyと呼ばれている。以下は、これらの分野と実際のアプリケーションの一般的なリストです。
近赤外:タンパク質、脂肪、低分子炭化水素、水などの化学種を定量的に測定することができる。さらに農産物、食品、石油、化学工業で利用が得られる
中赤外:最もポピュラーな赤外領域で、有機化合物や生化学化合物の構造決定に使用される。
遠赤外:無機物研究への応用が期待されるが、あまり普及していない分野である
ラマン。無機・有機・生物系の定性・定量分析に使用され、IRの補完的な手法として用いられることが多い。
百科事典を検索する