プランク定数

背景

この記事で使用している記号
シンボル 意味 E エネルギー h プランク定数 k ボルツマン定数 c 光速 λ ほうしゃせんはちょう ν ほうしゃせんしゅうはすう T 絶対温度

1670年から1900年の間に、科学者たちは光の性質について議論しました。ある科学者は、光は何百万もの小さな粒子で構成されていると信じていました。他の科学者は、光は波であると信じていました。

光：波か粒子か？

1678年、クリスティアン・ホイヘンスは「光についての理論書」（Traité de la lumiere）を書きました。彼は、光は波でできていると考えていました。彼は、光は粒子から成り立っていると考えていましたが、2本のビームから出た光は互いに跳ね返らないので、光は粒子から成り立っていないと述べています。1672年、アイザック・ニュートンは『オプティクス』という本を書きました。彼は、光は赤、黄、青の粒子でできていると考えていましたが、これをコーパスルと呼びました。ニュートンはこれを「2つのプリズム実験」で説明しました。最初のプリズムは光を異なる色に分解した。2つ目のプリズムは、これらの色を結合して白色の光に戻した。

18世紀には、ニュートンの理論が最も注目された。1803年、トーマス・ヤングは「二重スリット実験」を記述した。この実験では、2つの細いスリットを通過する光がそれ自体に干渉します。これは、光が波でできていることを示すパターンを引き起こします。19世紀の残りの期間、光の波動理論が最も注目されました。1860年代には、ジェームズ・クラーク・マクスウェルが電磁波を波として記述する方程式を開発しました。

電磁波の理論では、光、電波、マイクロ波など多くの種類の波を、波長が異なる以外は同じものとして扱っています。私たちが目で見ることのできる光の波長は、だいたい400～600nmです。電波の波長は10mから1500m、マイクロ波の波長は約2cmです。真空中では、すべての電磁波は光の速さで移動します。電磁波の周波数は次式で与えられます。

ν = c λ {displaystyle \nu ={\frac {c}{C}{\lambda }}}}}。.

ここではシンボルを定義しています。

ブラックボディのラジエーター

すべての暖かいものは熱放射、つまり電磁放射を発しています。地球上のほとんどのものにとって、この放射は赤外域にありますが、非常に高温のもの（1000℃以上）は、可視光線、つまり光を発します。1800年代後半には、多くの科学者が、異なる温度の黒体放射器からの電磁波の波長を研究しました。

レイリージャン法

レイリー卿は1900年に初めてレイリー＝ジャンの法則の基礎を発表した。この理論は気体の運動論に基づいていました。ジェームス・ジーンズ卿は1905年に、より完全な理論を発表しました。法則は、異なる温度で黒体放射器によって与えられる電磁エネルギーの量と波長を関連付ける。これを記述する式は

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

長波長の放射線では、この式で予測された結果は実験室での実際の結果とよく一致していました。しかし、短波長（紫外光）では理論と実験の差が大きく、「紫外大災害」と呼ばれるようになりました。

プランクの法則

1895年、ウィーンは黒体からの放射線についての研究結果を発表しました。彼の公式は

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{2hc^{2}}{5}}}e^{-{\frac {hc}{lambda kT}}}}.

この式は短波長の電磁波に対してはよく機能しますが、長波長の電磁波に対してはよく機能しませんでした。

1900年、マックス・プランクは研究の成果を発表した。彼は、放射線が小さなクアンタからなると仮定して、そのクアンタを無限に小さくしたらどうなるかを見て、波長で表される黒体放射の式を開発しようとした（これは標準的な数学的アプローチである。これは標準的な数学的アプローチです）。式は次のようになりました。

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{lambda ^{5}}}~{\frac {1}{e^{frac {hc}{\lambda kT}}-1}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}。.

光の波長が非常に大きくなることが許されるならば、レーリー・ジャンとプランクの関係はほとんど同じであることがわかります。

彼はhとkを計算して、次のことを発見しました。

h = 6.55×10^-27エルグ・秒。

k = 1.34×10^-16 erg-deg-¹.

これらの値は、それぞれ6.62606×10^-34と1.38065×10^-16という現代の常識に近い値である。プランクの法則は実験データとよく一致していますが、その完全な意義が評価されたのは数年後のことでした。

光の量子論

光がしきい値の周波数に達すると、光電効果によって電子がはずれてしまうことがわかりました。これ以下では電子は金属から放出することができません。1905年にアルバートアインシュタインは、効果を説明する論文を発表した。アインシュタインは、光のビームは、空間を伝播する波ではなく、むしろ離散的な波のパケット（光子）のコレクションではなく、それぞれのエネルギーを提案した。アインシュタインは、効果は、電子を打つ光子のためだったと述べた。これは、光の粒子の性質を実証した。

また、アインシュタインは、波長の長い電磁波は効果がないことを発見しました。アインシュタインは、これは"粒子"が電子を乱すのに十分なエネルギーを持っていなかったためだと述べた。

プランクは、各光子のエネルギーは、プランク定数によって光子の周波数と関連していることを提案しました。これは数学的には次のように書くことができます

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{lambda }}}}}.

プランクは、エネルギー量子の発見によって物理学の進歩に貢献した功績が認められ、1918年にノーベル賞を受賞しました。1921年にアインシュタインは、光電効果にプランク定数をリンクするためのノーベル賞を受賞しました。

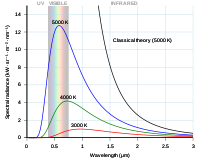
レイリー・ジャン曲線とプランクの曲線を光子の波長に対してプロットしたもの。


ソルウェイ会議1911。プランク、アインシュタイン、ジーンズが立っている。プランクは左から2番目。アインシュタインは右から2番目。ジーンズは右から5番目。Wienが座っていて、右から3番目


ニュートンの王立協会への手紙の原文（1671年1月1日[ユリウス暦]）から抜粋したイラスト。Sは太陽光を表す。平面BCとDEの間の光には色がある。これらの色が再結合して、平面GH上の太陽光を形成している。


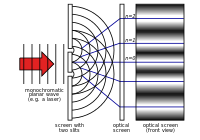
ヤングの二重スリット実験

アプリケーション

プランク定数は多くのアプリケーションで重要です。そのうちのいくつかを以下に示します。

ボーア原子モデル

1913年にニールス・ボーアは原子の構造のボーアモデルを発表しました。ボーアは、原子核の周りを回る電子の角運動量は一定の値しか持てないと言いました。これらの値は次の式で与えられます。

L = n h 2 π {displaystyle L=n{\frac {h}{2π }}}}}}}}}。

孰れ

L = レベルに関連する角運動量。

n = 正の整数。

h = プランク定数。

原子のボーアモデルでは、各レベルの電子のエネルギーを計算することができます。電子は通常、原子の最も低い番号の状態で満たされます。原子が例えば電流などのエネルギーを受けると、電子はより高い状態に励起されます。その後、電子は低い状態に戻り、光子を放出することで余分なエネルギーを失います。エネルギー準位が特定の値を持つので、光子は特定のエネルギー準位を持つことになります。このようにして放出された光は、プリズムを使って異なる色に分けることができます。それぞれの要素は独自のパターンを持っています。ネオンのパターンを横に示します。

ハイゼンベルクの不確定性原理

1927年、ヴェルナー・ハイゼンベルクは不確かさの原理を発表しました。この原理は、測定されているものを妨害することなく測定を行うことは不可能であるとしています。また、測定を行うことによって生じる最小の妨害にも制限を設けています。

巨視的な世界では、これらの外乱はほとんど違いがありません。例えば、液体のフラスコの温度が測定されている場合、温度計は、それが加熱されると、少量のエネルギーを吸収します。これは、最終的な読み取り値に小さな誤差が発生しますが、この誤差は小さく、重要ではありません。

量子力学では、物事は異なります。いくつかの測定は、散乱された光子のパターンを見ることによって行われます。そのような例の一つがコンプトン散乱です。粒子の位置と運動量の両方を測定する場合、不確かさの原理は、運動量を測定する精度と位置を測定する精度の間にトレードオフがあるとしています。このトレードオフを説明する式は次の通りです。

Δ x Δ p 笆笆謇譛ｬ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺ｭ縺

孰れ

Δp＝運動量の不確かさ

Δｘ＝位置の不確かさ

h = プランク定数。

発光ダイオードの色

右図の電気回路では、発光ダイオード（LED）の電圧降下はLEDの材質によって異なります。シリコンダイオードの場合、電圧降下は0.6 Vですが、LEDの場合は1.8 Vから2.7 Vです。この情報により、ユーザーはプランク定数を計算することができます。

1 つの電子が LED 材料の電位障壁をジャンプするのに必要なエネルギーは、次の式で与えられます。

E = Q e V L {displaystyle E=Q_{e}V_{L}V_{L}, }。

孰れ

_Qeは1個の電子にかかる電荷です。

_VLはLEDの電圧降下です。

電子が再び崩壊するとき、電子は1個の光の光子を放出します。この光子のエネルギーは、光電効果で使われるのと同じ式で与えられます。これらの式を組み合わせると、光の波長と電圧は次式で表されます。

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}}},｝。

この関係から下の表を計算することができます。

色	波長 (nm)	電圧
赤信号	650	1.89
グリーンライト	550	2.25
ブルーライト	470	2.62

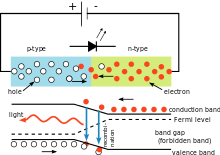
プランク定数の使用を説明するシンプルなLED回路。発光される光の色はダイオードの電圧降下に依存します。光の波長はプランク定数を使って計算できます。


ネオンの可視スペクトル。各線はエネルギーレベルの異なるペアを表しています。


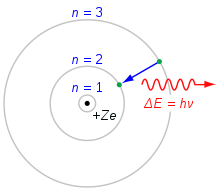
ボーアの原子モデル。n=3の殻からn=2の殻に落下する電子はエネルギーを失う。このエネルギーは1個の光子として持ち去られる。

プランク定数の値とキログラムの再定義

それが発見されて以来、hの測定ははるかに良くなってきました。プランクは最初にhの値を6.55×10^-27エルグ秒と見積もった。この値は現在の値の5%以内である。

2014年3月3日現在、hのSI単位での最適な測定値は、6.62606957×10^-34 J・sです。cgs単位での等価値は6.62606957×10^-27 erg-secです。hの相対的な不確かさは4.4×10^-8です。

還元プランク定数（ħ）は、量子力学で使われることもある値です。これは次のように定義されます。

症状が出た時には、「お腹が空いた」と言っていましたが、「お腹が空いた」と言っていました。.

量子力学では、SIではなくプランク単位が使われることがあります。この系では、還元されたプランク定数の値は1なので、プランク定数の値は2πとなります。

プランク定数は非常に高い精度で測定できるようになりました。このため、BIPMはキログラムの新しい定義を検討することになりました。国際的なプロトタイプのキログラムは、もはやキログラムの定義には使われていません。その代わりに、BIPMはプランク定数を正確な値を持つように定義しています。科学者たちは、この値とメートルと秒の定義を使ってキログラムを定義しています。

 

理論プランク定数の値

プランク定数も数学的に導き出すことができます。

 

h = μ 0 π 12 c 3 [ q 0 [ 0.9163 a 0 ] 2 ] 22 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J・s {\displaystyle h={\frac {\mu _{0}pi }{12c^{3}}}}{[{q_{0}}{[0.9163a_{0}]}^{2}] ^{2}}{f_{1r}}^{5}\cdot {s}=6.63Times 10^{34}J・s {\cdot s}.

ここで、μ 0 {displaystyle \mu _{0}}は自由空間の透過率、 c {\displaystyle c}は光の速さ、 q 0 {\displaystyle q_{0}}は電子の電荷、 a 0 {\displaystyle a_{0}はボーアの半径、 f 1 r {\displaystyle f_{1r}}は水素原子の中の電子の回転数 ( f 1 r = 3.29 × 10 15 r e v / s) {\displaystyle (f_{1r}=3.29times 10^{15}rev/s)} .これらの定数を理論プランク定数に代入すると、理論プランク定数の値は実験値と全く同じになる。

関連ページ

• 波動粒子二元性