度数分布の定義と例：統計学における頻度表・階級とヒストグラム
統計学において、度数分布とは、ある変数が標本でとる値と、その各値が出現する回数（度数）を一覧にしたものです。通常、値を数量順やカテゴリ順に並べ、各値に対応する度数を示します。度数分布はデータの全体像をつかむための基本的な整理法であり、中心位置・散らばり・偏り・異常値の発見に役立ちます。
例：5段階リッカート尺度の度数分布
たとえば、あるアンケートで100人に「同意」を5段階（1＝強く同意、5＝強く反対）で評価してもらった結果を整理すると、度数分布は次のようになります（例示データ）。
| 評価 | 度数 (f) | 相対度数 (f / N) |
|---|---|---|
| 1（強く同意） | 30 | 0.30（30%） |
| 2 | 25 | 0.25（25%） |
| 3 | 20 | 0.20（20%） |
| 4 | 15 | 0.15（15%） |
| 5（強く反対） | 10 | 0.10（10%） |
| 合計 | 100 | 1.00（100%） |
ここで相対度数は各度数を標本サイズ N（ここでは100）で割った値で、割合や確率的解釈を与えます。さらに累積度数（例えば「評価が3以下の人数」）を計算すると、分布の位置関係が分かりやすくなります。
連続変数や値の種類が多い場合：階級と度数表
しかし、変数が連続値をとる場合や、取り得る値の種類が非常に多い場合には、個々の値ごとに度数を示すのは現実的でないことが多いです。こうした場合は、値の範囲をいくつかの区間（階級, class interval）に分け、それぞれの階級に入る観測の数を数えます。これを階級幅と呼びます。
身長（cm）を例にした階級別度数表：
| 階級 (cm) | 度数 (f) | 相対度数 | 累積度数 |
|---|---|---|---|
| 140–149 | 2 | 0.04 | 2 |
| 150–159 | 8 | 0.16 | 10 |
| 160–169 | 20 | 0.40 | 30 |
| 170–179 | 15 | 0.30 | 45 |
| 180–189 | 5 | 0.10 | 50 |
| 合計 | 50 | 1.00 | — |
このように階級ごとにまとめることで、連続データの分布が視覚的にも把握しやすくなります。
ヒストグラムと棒グラフの違い
階級別度数を図示する代表的な方法がヒストグラムです。ヒストグラムでは横軸に階級、縦軸に度数または相対度数を取り、各階級を幅のある長方形で表します。連続データでは階級の長方形の間に隙間は置かれません（階級幅が視覚的に重要）。一方、カテゴリデータの棒グラフでは棒同士に隙間を設けるのが一般的です。
関連する指標と計算式
- 相対度数：r_i = f_i / N（各階級・カテゴリの度数を総数で割る）
- 累積度数：F_k = Σ_{i≤k} f_i（ある値以下またはある階級までの合計度数）
- 度数密度（階級幅が一定でないとき）：度数密度 = f_i / 幅（ヒストグラムの高さを比率で調整するために用いる）
階級幅や階級数の決め方のヒント
- 経験則としての方法：Sturgesの公式 k ≈ 1 + log2(N)（階級数の目安）
- データのばらつきに応じた方法：Freedman–Diaconis の法則（ビン幅 = 2 × IQR × N^(−1/3)）は中央値周りの広がり（IQR）を利用する
- 階級幅は等間隔にするのが扱いやすいが、データの分布に合わせて可変幅を使うこともある
- 階級の端点（端数の切り上げ・切り下げ）によって度数が変わるので、境界の取り方は明示する
度数分布を使う理由と注意点
- データの中心（平均・中央値）や散らばり（分散・標準偏差）が直感的に理解しやすくなる。
- 分布の形（左右の偏り、山の数、裾の重さ）や外れ値の存在を視覚的に確認できる。
- 階級分けの仕方によって見え方が変わるため、比較する際は同じ階級設定を使うことが重要。
- 度数分布は元データの情報を要約するものであり、細部の情報は失われる可能性がある（階級化による情報の粗度）。
以上が度数分布の基本的な定義と利用法、具体例です。データの性質（離散か連続か、サンプルサイズ、解析目的）に応じて、元の個々の値を並べるか、階級にまとめるかを選んでください。
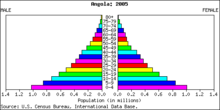
(絶対)度数分布の例。これは、2005年のアンゴラの人口ピラミッドです。
これは、2005年の中国の人口ピラミッドです。
アプリケーション
頻度集計されたデータの管理・操作は、生データに対する操作に比べ、はるかに簡単です。中央値、平均値（統計量）、標準偏差などを計算する簡単なアルゴリズムがあります。
統計的仮説検定は、度数分布間の差異と類似性を評価することに基づいている。この評価には、平均値や中央値などの中心傾向や平均値の測定と、標準偏差や分散などの変動性や統計的分散の測定が含まれます。
度数分布は、平均値と中央値が異なる場合、「歪んでいる」と言われます。度数分布の尖度とは、平均値への得点の集中度、あるいはヒストグラムなどでグラフ化したときに分布がどの程度尖って見えるかを表します。分布が正規分布よりも尖っている場合はレプトカーティック、尖っていない場合はプラティカーティックと呼ばれます。
頻度分布は、暗号を解読するための周波数解析にも使われ、異なる言語における文字の相対的な頻度を指す。
質問と回答
Q:度数分布とは何ですか?
A:度数分布とは、ある変数がサンプルでとる値を数量順に並べたリストです。各値が何回現れるかを示しています。
Q:5点リッカート尺度の回答の度数分布は、どのように見えますか?
A: 5点リッカート尺度の回答の度数分布は、尺度上の各点を評価した人の数を示す単純な表のように見えるかもしれません。
Q: このタイプの表を使用することの2つの欠点は何ですか?
A: このタイプの表を使用する2つの欠点は、連続的な値を扱うとき、または可能な値が多すぎるときに、困難または不可能になる可能性があることです。
Q:連続値や多数の可能な値を扱う場合、この方式はどのように違うのですか?
A:連続的な値や多数の値を扱う場合は、値の範囲に基づく少し異なる方式を代わりに使用することができます。
Q: 学生の身長の度数表はどのように見えますか?
A: 学生の身長の度数表は、範囲と何人の学生がそれぞれの範囲に入るかを示すかもしれません。
Q:度数分布は、どのような情報を提供しますか?
A:度数分布は、特定の変数が標本に現れる頻度、およびそれらの標本間でどのように分布しているかについての情報を提供します。
