ヒストグラム

ヒストグラムは、統計学の概念です。これは、関係するサンプルの分布について教えてくれるグラフ表示です。ヒストグラムは、多くのカテゴリーを持つ表から作られた図が一般的です。表には、各カテゴリーにいくつのサンプルがあるかが書かれています。

ヒストグラムという言葉は、ギリシャ語のヒストスとグランマに由来しています。ヒストスは網やマストという意味です。グランマは描画、記録、書き込みという意味です。したがって、何かのヒストグラムは、語源的に言えば、この何かの網の図面です。

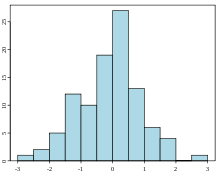
正規分布する100個の乱数値からなるヒストグラムの例

類似のアイデア

ヒストグラムは、品質管理の7つの基本ツール（パレート図、チェックシート、管理図、因果関係図、フローチャート、散布図など）の一つです。

ヒストグラムの一般化として、カーネルスムージング技術があります。これは、供給されたデータから滑らかな確率密度関数を構築するものです。

A: ヒストグラムは、関係するサンプルの分布を示すグラフ表示です。

A: ヒストグラムの目的は，関係する標本の分布を示すことです。

A: ヒストグラムの語源はギリシャ語のヒストス（histos）とグランマ（gramma）です。ヒストスは網やマストを意味します。グランマは図面、記録、文章を意味します。

A: "histos "はギリシャ語で網やマストを意味します。

A: 「gramma」とはギリシャ語で「描く」「記録する」「書く」という意味です。

A: ヒストグラムの一般的な特徴は、多くのカテゴリーを持つ表から作られた画像です。

A: ヒストグラム表は、各カテゴリーにいくつのサンプルがあるかという情報を提供します。