標準偏差とは:定義・計算式・解釈と実例でわかる統計入門
標準偏差とは何かを定義・計算式・解釈・実例で丁寧に解説。初心者でもわかる図解と計算手順付きの統計入門。
標準偏差とは、あるグループの測定値が平均値からどの程度ばらついているかを表す数値です。標準偏差が小さいと、ほとんどの数値が平均に近く、標準偏差が大きいと値が広く分散していることを意味します。単位は元のデータと同じで、分散(各値と平均の差の二乗の平均)の平方根として定義されます。
定義と種類
母標準偏差(population standard deviation)と標本標準偏差(sample standard deviation)の二種類があります。
- 母標準偏差(σ):データが母集団全体(全数)であるときに使います。式は σ = sqrt( (1/N) Σ (xi − μ)² ) です。
- 標本標準偏差(s):母集団の一部(サンプル)しか測れないときに使います。分母に n−1 を使うことで母分散の不偏推定量とする補正(ベッセルの補正)を行います。式は s = sqrt( (1/(n−1)) Σ (xi − x̄)² ) です。
なぜ n−1 を使うのか(ベッセルの補正)
標本から母分散を推定する際、標本平均 x̄ を使うと分散の期待値が実際の母分散を過小評価する傾向があります。この偏りを補正するために分母を n−1 にして不偏推定量にします。小さな標本サイズほど影響が大きくなります。
計算の手順(簡単な例)
データ:2, 4, 4, 4, 5, 5, 7, 9
- 平均 x̄ = (2+4+4+4+5+5+7+9) / 8 = 5
- 各値と平均との差(偏差):−3, −1, −1, −1, 0, 0, 2, 4
- 偏差の二乗:9, 1, 1, 1, 0, 0, 4, 16 → 合計 = 32
- 母分散 = 32 / 8 = 4 → 母標準偏差 σ = sqrt(4) = 2
- 標本分散 = 32 / (8−1) ≈ 4.5714 → 標本標準偏差 s ≈ 2.138
解釈と実用例
- 標準偏差が小さい:データが平均の周りに集中している。測定のばらつきが小さいことを示す。
- 標準偏差が大きい:データが平均から遠く離れている値を含みやすい。ばらつきが大きい。
- 正規分布(ガウス分布)の場合、経験則として約68%が±1σ、約95%が±2σ、約99.7%が±3σの範囲に入る(68-95-99.7ルール)。このため「報告される誤差は、通常、標準偏差の2倍です」といった表現は、正規分布を仮定したときに95%程度の範囲を示す便利な近似です。
- 科学者は実験の平均値と標準偏差を報告し、平均値と比較して2〜3σ以上の差を統計的に重要とみなすことが多い(ただし厳密には検定やp値など別の判断が必要)。
- 金融分野では標準偏差は「ボラティリティ(変動性)」の指標として使われます。例えば利子や投資リターンの標準偏差が大きいと、個々の人や資産の得る利子やリターンが平均から大きくずれることを意味します(お金の分野での応用)。
関連の指標と注意点
- 標準誤差(standard error):平均の推定精度を表す指標で、標準誤差 = σ / sqrt(n)(標本の場合は s / sqrt(n))です。標準偏差とは別の意味を持ちます。
- 変動係数(CV):平均に対する相対的なばらつきは CV = σ / μ で表します。平均が異なるデータセット同士を比較する際に便利です。
- 標準偏差は外れ値に敏感です。データに外れ値が多い場合は四分位範囲(IQR)などのロバストな指標の併用を検討してください。
- 分布が正規分布でないときは、±2σが95%を必ず保証するわけではありません。分布の形に応じた解釈が必要です。
まとめ
標準偏差はデータの散らばりを直感的に示す重要な統計量です。母集団全体を扱うときは σ(分母 N)、標本から母集団を推定するときは s(分母 n−1)を使います。実際の解析では、標準偏差だけでなく分布の形、外れ値の有無、標本サイズ、標準誤差なども併せて考えることが大切です(例として研究での報告や、科学者のデータ解析、サンプルからの推定、金融のボラティリティ評価などに広く使われます)。
.png)
正規分布(またはベルカーブ)をプロットしたもの。各色の帯は1標準偏差の幅を持つ。
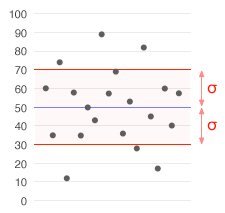
平均値が50(青で表示)、標準偏差(σ)が20のデータセット。
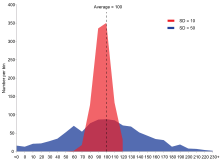
同じ平均値と異なる標準偏差を持つ2つのサンプル集団の例。赤の集団は平均100、SD10、青の集団は平均100、SD50。
基本例
以下の8つの数字を持つグループを考えてみましょう。
22,4,4,544455,7,9
この8つの数字の平均値は5である。
24557+ + + + + + + = {{displaystyle {}} {2+4+4+5+5+7+9}{8}}=544985}となります。
母集団の標準偏差を計算するには、まず、リストの各数値の平均値からの差を求めます。次に、それぞれの差の結果を2乗します。
( 2-5 ) =2 ( -3 ) = 2(95 - 5) = 2022(04 - 15) = 2(15 -5 ) = 202( 04-5 ) = 2( -1 ) = 22(17 - 55) = 22( 44- ) = 2( 1242- ) = ( - ) = ( - ) = ={{195216array}{lll}(2-5)^{2}=(-3)^{2}=9&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(5-5)^{2}=0^{2}=0\\(4-5)^{2}=(-1)^{2}=1&&(7-5)^{2}=2^{2}=4\\(4-5)^{2}=(-1)^{2}=1&&(9-5)^{2}=4^{2}=16\\\end{array}}}
次に、これらの値の平均値(和÷数字の数)を求めます。最後に、平方根をとります。
( +9 + 100416+ + + + + ) = {\\ {(11829+1+1+1+0+4+16)}{8}}=2}となります。
答えは「母集団標準偏差」です。この式が成り立つのは、最初に挙げた8つの数字がグループ全体のものである場合だけです。もし、無作為に選ばれたグループの一部だけであれば、最後から2番目のステップの下(分母)に8(n)ではなく、7(n-1)を使うべきです。すると、答えは標本標準偏差となります。これをBessel's Correctionといいます。
その他の例
少し難しい実例です。米国の成人男性の平均身長は70インチで、標準偏差は3インチです。標準偏差が3インチということは、ほとんどの男性(正規分布を仮定した場合、約68%)の身長が平均値(67インチ〜73インチ)よりも3インチ高いか3インチ低い、つまり1つの標準偏差ということになります。ほぼすべての男性(約95%)の身長は、平均値(64インチ~76インチ)よりも6インチ高く、6インチ低く、つまり2つの標準偏差があります。3つの標準偏差は、調査対象となるサンプル集団の99.7%のすべての数値を含みます。これは、分布が正規(ベル型)の場合に当てはまります。
もし標準偏差がゼロならば、すべての男性の身長はちょうど70インチになります。標準偏差が20インチであれば、一部の男性は平均よりもはるかに背が高く、またははるかに低く、典型的な範囲は約50インチ~90インチとなります。
別の例では、{0, 0, 14, 14}、{0, 6, 8, 14}、{6, 6, 8, 8}の3つのグループのそれぞれの平均(平均)は7ですが、標準偏差は7、5、1です。基本的な考え方は、標準偏差は、残りの数字が平均からどれだけ離れているかを教えてくれます。標準偏差の単位は、数字と同じです。例えば、{0, 6, 8, 14}というグループが4人の兄弟の年齢を年で表している場合、平均は7年、標準偏差は5年です。
標準偏差は、不確実性の尺度として用いられることがあります。例えば、科学の分野では、繰り返し行われる測定の標準偏差は、科学者が平均的な数値をどの程度確信しているかを知るのに役立ちます。実験で得られた測定値が予測と一致するかどうかを判断する際、それらの測定値の標準偏差は非常に重要です。実験で得られた平均的な数値が予測された数値からあまりにも離れている場合(その距離は標準偏差で測定されます)、検証されている理論は正しくないかもしれません。予測区間を参照。
応用例
一連の値の標準偏差を理解することの用途は、「平均」(mean)からどの程度の差が予想されるかを知ることにあります。
天気予報
簡単な例として、内陸部と海に近い場所にある2つの都市の1日の平均最高気温を考えてみましょう。海に近い都市の日最高気温の範囲は、内陸部の都市よりも小さいことを理解しておくとよいでしょう。この2つの都市は、それぞれ同じ日最高気温の平均値を持つかもしれない。しかし、沿岸部の都市の一日の最高気温の標準偏差は、内陸部の都市のそれよりも小さくなります。
スポーツ
別の見方をすれば、スポーツチームを考えてみましょう。どんなスポーツでも、得意なチームと不得意なチームがあります。上位にランキングされたチームは、能力の差があまり見られません。ほとんどのカテゴリーで良い成績を残します。各カテゴリーの能力の標準偏差が低いほど、バランスが取れていて一貫性があります。しかし、標準偏差が高いチームは、予測がつきにくくなります。ほとんどのカテゴリーで普段から悪い成績を残しているチームは、標準偏差が低くなります。ほとんどのカテゴリーで普段から良い成績を収めているチームは、標準偏差も低くなります。しかし、標準偏差が高いチームは、多くのポイントを獲得する(オフェンスが強い)一方で、相手チームに多くのポイントを取らせてしまう(ディフェンスが弱い)タイプのチームかもしれません。
どのチームが勝つかを事前に知るためには、様々なチームの "統計 "の標準偏差を見るとよいでしょう。予想と異なる数値は、強みと弱みを一致させ、どちらのチームが勝つかを知る上で最も重要な理由を示すことができます。
レースでは、ドライバーがコースを1周するのにかかった時間を計測する。ラップタイムの標準偏差が小さいドライバーは、標準偏差が大きいドライバーよりも安定しています。この情報は、ドライバーが1周するのにかかる時間を短縮する方法を理解するのに役立ちます。
マネー
お金の世界では、標準偏差は、価格が上下するリスクを意味する場合があります(株式、債券、不動産など)。また、価格のグループが上昇または下降するリスクを意味する場合もあります(アクティブ運用のミューチュアル・ファンド、インデックス・ミューチュアル・ファンド、またはETF)。リスクは、何を買うかを決定する一つの理由となります。リスクは、人々がどれだけのお金を得たり失ったりする可能性があるかを知るために使用できる数字です。リスクが大きくなればなるほど、投資のリターンは期待以上のものになる可能性があります(標準偏差の「プラス」)。一方で、予想以上に損失を被ることもあります(標準偏差マイナス)。
例えば、ある人が2つの銘柄を選ぶことになったとします。過去20年間の株式Aの平均リターンは10%で、標準偏差は20%ポイント(pp)でした。一方、銘柄Bの過去20年間の平均リターンは12%ですが、標準偏差は30ppと高くなっています。リスクを考えると、株式Aの方が安全だと判断する人もいるでしょう。儲けは少なくても、損失も少ないだろう。その人は、株式Bの平均値が2ポイント高いことは、標準偏差が10pp増えること(より大きなリスクや期待リターンの不確実性)に見合わないと考えるかもしれません。
正規分布する数値のルール
標準偏差の計算式の多くは、数値が正規分布していることを前提としています。これは、数字が平均値の両側にある一定の方法で広がっていることを意味します。正規分布は、カール・フリードリヒ・ガウスが発見したことから、ガウス分布とも呼ばれています。また、数値が広がっていく様子がグラフ上でベルの形をしていることからベルカーブと呼ばれることもあります。
数字が平均値の片側または反対側にまとまっていると正規分布ではない。数字が広がっていても、正規分布になります。標準偏差は、数値がどの程度広がっているかを示します。

紺色は、平均からの標準偏差が1以下の場合。正規分布の場合、これは68.27パーセントの数字を含み、平均から2つの標準偏差(中と紺)は95.45パーセントを含み、3つの標準偏差(薄、中、紺)は99.73パーセントを含み、4つの標準偏差は99.994パーセントを占めます。
平均値(平均)と標準偏差の関係
一連のデータの平均値(平均)と標準偏差は、通常、一緒に書かれる。そうすることで、平均的な数値が何であるか、またグループ内の他の数値がどれくらい広く分布しているかを理解することができます。
また、数値群の広がり方は、標準偏差を平均値で割った変動係数で表すことができます。これは無次元の数値である。変動係数は、しばしば100%を乗じて、パーセンテージとして表記されます。
沿革
標準偏差という言葉は、1894年にカール・ピアソンが講義で使った後、文章で初めて使った。これは、ガウスが平均誤差を使っていたように、同じ考えを表す以前の名前に代わるものでした。
関連ページ
- 正確さと精度
- サンプルサイズ
質問と回答
Q:標準偏差とは何ですか?
A:標準偏差とは、あるグループの測定値が平均値(平均値または期待値)からどのように広がっているかを示すために使用される数値です。
Q:標準偏差が低いとはどういう意味ですか?
A: 低い標準偏差は、ほとんどの数値が平均に近いことを意味します。
Q:高い標準偏差とはどういう意味ですか?
A:標準偏差が高いということは、数値がより分散していることを意味します。
Q:標準偏差はお金でどのように使われるのですか?
A:お金では、利息の標準偏差は、ある人の利息が平均とどれくらい違うかを示します。
Q:集団の一部しか測定できない場合とは?
A:多くの場合、サンプル、またはグループの一部のみが測定されます。
Q:グループ全体の標準偏差はどのように表されますか?
A:グループ全体の標準偏差はギリシャ文字のَで表されます。.
Q:標本の標準偏差はどのように表現されますか?
A:標本の標準偏差は s {displaystyle s} で表されます。
百科事典を検索する



