テイラー展開（テイラー級数）とは？定義・公式・導出・応用例とマクローリン級数

テイラー級数とは、コンピュータサイエンス、微積分、化学、物理、その他の高等数学で用いられる考え方です。ある関数がどのような形をしているかの推定値（推測値）を作成するために使用される級数である。テイラー級数には、マクロリン級数という特殊なものもあります。

テイラー級数の背後にある理論は、座標平面（x軸とy軸）上にある点を選択すると、その点の周りの領域で関数がどのように見えるかを推測することができるというものです。これは、関数の導関数を取り、それらをすべて足すことで行われます。これは、無限にある導関数を足して、1つの有限の和にすることができるということです。

数学では、テイラー級数とは、ある関数を無限級数の和として表したものです。和の項は、関数の微分から取られます。テイラー級数は、テイラーの定理に由来します。

定義と公式

関数 f が点 a のまわりで十分に微分可能であるとき、その点 a に関するテイラー級数は次の形で表されます。

f(x) = Σ_{n=0}^∞ [f^{(n)}(a) / n!] · (x − a)^n

ここで f^{(n)}(a) は f の n 階導関数を a で評価した値、n! は n の階乗です。特に a = 0 のときの級数をマクローリン級数（Maclaurin series）と呼びます。

テイラー多項式と剰余項（誤差）

n 次まで打ち切った多項式（テイラー多項式）は次のように定義されます。

P_n(x) = Σ_{k=0}^n [f^{(k)}(a) / k!] · (x − a)^k

元の関数 f(x) は P_n(x) に剰余項 R_n(x) を加えたものになります。

f(x) = P_n(x) + R_n(x)

剰余項の代表的な形（ラグランジュの剰余）は次の通りです：

R_n(x) = f^{(n+1)}(ξ) / (n+1)! · (x − a)^{n+1}（ある ξ が a と x の間に存在）

また、剰余の積分表示など別の表現もあり、これらを用いて近似誤差の評価ができます。

収束性と解析関数

テイラー級数がその中心 a の近傍で実際に f(x) に収束するかどうかは重要です。一般に、級数の収束半径 R は比率判定法や根判定法で求められます。収束半径が有限の場合、|x − a| < R の内部で級数は収束します（複素解析の観点では円板内で収束）。

ただし、関数が無限回微分可能（C^∞）であっても、必ずしもそのテイラー級数が元の関数に一致する（＝解析関数である）とは限りません。代表例として、x ≠ 0 のとき f(x) = exp(−1/x^2)、f(0) = 0 はすべての階導関数が 0 になりマクローリン級数は 0 だが、関数そのものは 0 ではありません（C^∞ だが解析的ではない）。一方、実解析・複素解析でいう「解析関数（analytic）」であれば、その点でのテイラー級数が関数に一致します。

代表的なマクローリン展開（例）

  • e^x = Σ_{n=0}^∞ x^n / n! （収束範囲：全実数）
  • sin x = Σ_{n=0}^∞ (−1)^n x^{2n+1} / (2n+1)! （全実数）
  • cos x = Σ_{n=0}^∞ (−1)^n x^{2n} / (2n)! （全実数）
  • 1 / (1 − x) = Σ_{n=0}^∞ x^n （収束範囲：|x| < 1）
  • ln(1 + x) = Σ_{n=1}^∞ (−1)^{n−1} x^n / n （収束範囲：−1 < x ≤ 1、条件付き収束を含む）

導出の要点（直感的な説明）

関数をある点の周りで多項式で近似することを考え、各次数について一致させるために導関数の値を係数に使います。すなわち、P_n の 0 次から n 次までの導関数を a で評価すると f の対応する導関数と一致するように係数を定めると、上に示した一般項が導かれます。テイラーの定理はこの近似と剰余項の存在を保証します。

応用例

  • 関数の近似と数値計算（例えば e^x や三角関数をコンピュータで評価する）
  • 微分方程式の級数解（級数法）
  • 物理での摂動展開や近似解析（小さなパラメータに対する展開）
  • 最適化やニュートン法など根の探索での局所近似（一次あるいは二次近似）
  • テイラー展開を使った誤差見積もり（数値積分や差分近似の精度評価）

注意点と補足

  • テイラー級数の有用性は、収束範囲と剰余の評価に依存します。実際の計算では打ち切り次数と剰余の大小を考慮します。
  • 複素平面では解析関数はその中心のまわりで必ずテイラー展開を持ち、収束半径は最寄りの特異点までの距離と一致します。
  • 実務ではマクローリン展開（a = 0）を使うことが多いですが、近似したい点の近傍に中心を置く方が少ない次数で高精度が得られることがあります。

以上がテイラー級数（およびマクローリン級数）の定義、公式、導出の要点、収束性、代表例と応用の概観です。具体的な関数ごとの収束性や剰余の評価は個別に検討する必要があります。

Zoom

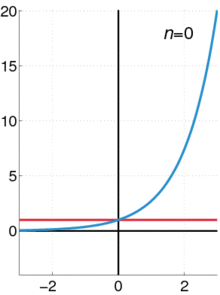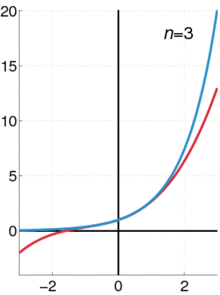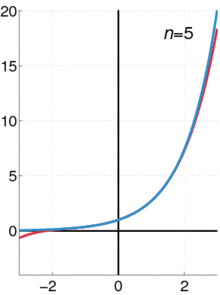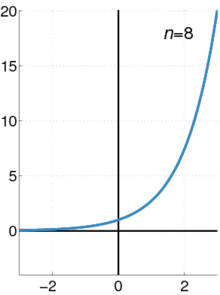
テイラー級数を使って関数を近似する方法を示したアニメーションである。青い線は、指数関数f ( x ) = e x {\displaystyle f(x)=e^{x}}を示している。{\displaystyle f(x)=e^{x}}.赤い線は、n個の微分の合計、つまりテイラー級数のn+1項を示している。nが大きくなると、赤線は青線に近づいていく。

沿革

このシリーズを最初に思いついたのは、古代ギリシャの哲学者、エレアのゼノンでした。ゼノンのパロドックス」と呼ばれるパラドックスがその結果である。彼は、無限の値を足して、結果として単一の有限の値を得ることは不可能であると考えた。

ギリシャの哲学者アリストテレスも、この哲学的な問いに対する答えを出していた。しかし、数学的な解決策を導き出したのは、アルキメデスの「消耗法」であった。アルキメデスは、何かを無限に細かく分割しても、それらをすべて足せば1つの全体になることを証明した。その数百年後、古代中国の数学者である劉輝が同じことを証明した。

テイラー級数の最も古い例は、1300年代にインドのサニャガマーグラマのマードヴァの研究であると言われています。後のインドの数学者たちは、サイン、コサイン、タンジェント、アークタンジェントの三角関数に関する彼の研究について書いている。マードラバの著作や記録は現在では残っていない。他の数学者たちは、マードゥワヴァの発見に基づいて、1500年代までこれらの系列の研究を進めた。

スコットランドの数学者であるJames Gregoryは、1600年代にこの分野で活躍しました。グレゴリーはテイラー級数を研究し、いくつかのマクローリン級数を発表した。1715年、ブルック・テイラーは、この級数をすべての関数に適用する一般的な方法を発見した。(それまでの研究では、特定の関数だけに適用する方法しか知られていなかった）。Colin Maclaurinは、1700年代にテイラー級数の特殊なケースを発表した。このゼロを中心とした級数をマクラウリン級数と呼ぶ。

定義

テイラー級数は、平滑関数（数学用語では「無限微分可能」）である任意の関数 ƒ（x）を記述するために使用できます。テイラー級数は、関数がある数aの近傍でどのように見えるかを記述するために使用されます。

このテイラー級数は、冪級数として書くと次のようになります。

f ( a ) + f ′ ( a ) !1( x - a ) + f ″ ( a ) !2( x - a ) +2 f 3( ) ( a ) !3( x - a ) + ⋯ 。3{\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots .} {\displaystyle f(a)+{\frac {f'(a)}{1!}}(x-a)+{\frac {f''(a)}{2!}}(x-a)^{2}+{\frac {f^{(3)}(a)}{3!}}(x-a)^{3}+\cdots .}

この式は、シグマ表記では次のようにも書けます。

∑ n 0= ∞ f ( n ) ( a ) n !( x - a ) n {\\_sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}˶,(x-a)^{n}} {\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(a)}{n!}}\,(x-a)^{n}}

ここで、n！はnの階乗である。 ƒ (n)(a)は点aにおけるƒのn次導関数であり、a{displaystyle a}aは関数の領域内の数である。ある関数のテイラー級数がその関数と等しい場合、その関数は "解析的関数 "と呼ばれる。

マクラウリンシリーズ

a = {0displaystyle a=0}のとき{\displaystyle a=0}のとき、その関数はマクローリン級数と呼ばれる。マクラウリン級数をべき乗級数として書くと次のようになる。

f 0( ) + f0 ′ ( ) !1x + f ″ ( ) !02x +2 f 30( ) ( ) !3x + ⋯ .3{\displaystyle f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f^{(3)}(0)}{3!}}x^{3}+\cdots .} {\displaystyle f(0)+{\frac {f'(0)}{1!}}x+{\frac {f''(0)}{2!}}x^{2}+{\frac {f^{(3)}(0)}{3!}}x^{3}+\cdots .}

シグマ記法で書くと、マクローリン級数は

∑n 0= ∞ f ( n ) ( )0 n !x n { {sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!｝ {\displaystyle \sum _{n=0}^{\infty }{\frac {f^{(n)}(0)}{n!}}\,x^{n}}

共通テイラー級数

いくつかの重要なTaylorシリーズとMaclaurinシリーズは以下の通りです。

sin x = ∑ n 0= ∞ ( - )1 n ( n 21+ ) !x n 2+ = 1x - x !33+ x !55- ⋯ for all x {\sin x==sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots {\text{ for all }}x\!} {\displaystyle \sin x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-\cdots {\text{ for all }}x\!}

cos x = ∑ n 0= ∞ ( - )1 n ( n2 ) !x n 21= - x !22+ x !44- ⋯ for all x {˶ˆ꒳ˆ˵} {sum _{n=0}^{˶ˆ꒳ˆ˵} {˶ˆ꒳ˆ˵} {x^{2n}=1-{˶ˆ꒳ˆ˵}+{˶ˆ꒳ˆ˵} {x^{4}}{4}-˶ˆ꒳ˆ˵} {˶ˆ꒳ˆ˵} {x^{4}}{4}}-˶ˆ꒳ˆ˵} { for all }}x\!} {\displaystyle \cos x=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-\cdots {\text{ for all }}x\!}

sinh ( x ) = ∑n 0= ∞ (1 n2 + ) !1x n 2+ for1 all x {\sinh(x)=\_sum _{n=0}^{\infty }{\frac {1}{(2n+1)!}}x^{2n+1}{\text{ for all }}x\!} {\displaystyle \sinh(x)=\sum _{n=0}^{\infty }{\frac {1}{(2n+1)!}}x^{2n+1}{\text{ for all }}x\!}

cosh ( x ) = ∑n 0= ∞ (1 n2 ) !x n 2for all x {displaystyle ˶ˆ꒳ˆ˵ }{sum _{n=0}^{˶ˆ꒳ˆ˵ }{frac {1}{(2n)!}}x^{2n}{text{ for all }}x\!} {\displaystyle \cosh(x)=\sum _{n=0}^{\infty }{\frac {1}{(2n)!}}x^{2n}{\text{ for all }}x\!}

e x = ∑ n 0= ∞ n 1!x n = +1 x + !12x + !213x + ⋯3 for all x {displaystyle e^{x}=Sum _{n=0}^{\infty }{1}{n!}}x^{n}=1+x+{frac {1}{2!}}x^{2}+{frac {1}{3!}}x^{3}+\cdots {text{ for all }}x\!} {\displaystyle e^{x}=\sum _{n=0}^{\infty }{\frac {1}{n!}}x^{n}=1+x+{\frac {1}{2!}}x^{2}+{\frac {1}{3!}}x^{3}+\cdots {\text{ for all }}x\!}

11 -  x = ∑ n 0= ∞ x n = +1 x + 2x + 3x 4+ ⋯ for all | x | < {1˶ˆ꒳ˆ˵}=sum _{n=0}^{˶ˆ꒳ˆ˵}x^{n}=1+x+x^{2}+x^{3}+x^{4}+cdots {˶ˆ꒳ˆ˵}|x|<1} {\displaystyle {\frac {1}{1-x}}=\sum _{n=0}^{\infty }x^{n}=1+x+x^{2}+x^{3}+x^{4}+\cdots {\text{ for all }}|x|<1}

ln ( +1 x ) = ∑ n 1= ∞ ( - )1 n + n1 x n for all | x 1| < {\displaystyle ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}{ for all }}|x|<1}}。 {\displaystyle \ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}{\text{ for all }}|x|<1}

tan x = ∑ n 1= ∞ B n 2( - )4 n 1( -4 n ) ( n2 ) !x n 2- =1 x + x 2515+ ⋯33 for | x | < π {\\\\tan x=sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}=x+{\\ {x^{3}}{3}}+{\ {2x^{5}}{15}}+cdots {text{ for }}|x|<{\ {pi }{2}}\!}2 {\displaystyle \tan x=\sum _{n=1}^{\infty }{\frac {B_{2n}(-4)^{n}(1-4^{n})}{(2n)!}}x^{2n-1}=x+{\frac {x^{3}}{3}}+{\frac {2x^{5}}{15}}+\cdots {\text{ for }}|x|<{\frac {\pi }{2}}\!}

ここで、B n {displaystyle B{\displaystyle B_{n}}_{n}}は、n番目のベルヌーイ数であり、ln {displaystyle ˶ln}は自然対数で{\displaystyle \ln }ある。

質問と回答

Q: テイラー級数とは何ですか?


A: テイラー級数はコンピュータ科学、微積分学、化学、物理学、その他の高等数学で使用される考え方です。ある関数がどのように見えるかの推定（推測）を作成するために使用される級数です。

Q: Taylor級数とMaclaurin級数の違いは何ですか?


A: マクローリン級数という特殊なテイラー級数もあります。

Q: テイラー級数の背後にある理論は何ですか?


A: テイラー級数の理論は、座標平面（x軸とy軸）上にある点を選ぶと、その点の周りの領域で関数がどのようになるかを推測することができるというものです。

Q: テイラー級数を使って関数はどのように作られるのですか?


A: これは関数の導関数をとり、それらをすべて足し合わせることによって行われます。無限にある導関数を足し合わせれば、1つの有限の和になるという考え方です。

Q: テイラー級数は数学で何を示すのですか?


A: 数学では、テイラー級数は関数を無限級数の和として示します。和の項は関数の導関数から取られます．

Q: テイラー級数はどこから来たのですか?


A: テイラー級数はテイラーの定理に由来します．

Q: テイラー級数はどの分野でよく使われますか?


A: テイラー級数はコンピュータサイエンス，微積分，化学，物理，その他の高等数学でよく使われます．

AlegsaOnline.com - 2020 / 2025 - License CC3