乗算（掛け算）とは？定義・性質・図と例でやさしく解説

乗算（掛け算）の定義と性質を図と具体例でやさしく解説。可換性や実数・行列の違いも図解で理解できる、初学者向けの完全ガイド。

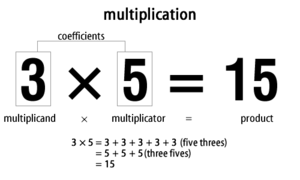
乗算（掛け算）とは

乗算は、2つの数字の積を求める算術の一つで、四則演算（加法・減法・乗法・除法）の基本操作のひとつです。一般に「掛ける」「〜倍する」といった表現で使われます。乗算の結果は「積」と呼ばれ、掛けられる側を被乗数、掛ける側を乗数といいます（英語では multiplicand, multiplier）。

自然数・面積・スケーリングとしての見方

自然数の場合、乗算は「繰り返しの加算」として理解できます。例えば3×5は「5を3回足す」または「3を5回足す」であり、どちらも15になります（5+5+5 = 3+3+3+3+3 = 15）。この考えは数の直感的な意味づけに役立ちます（繰り返しの加算の説明は基数の乗算にも関連します）。

また、自然数の乗算は、ある長方形のタイルの並びを数えることで視覚化できます。片方の辺にタイルが3列、もう片方の辺に5行ある長方形には3×5個のタイルが並びます。さらに、実数の乗算は一辺の長さが第1の数、もう一方の辺の長さが第2の数であるような長方形の面積（面積を求める操作）として解釈できます。

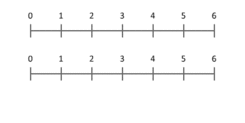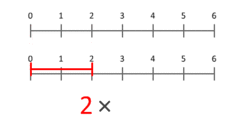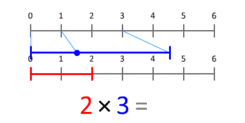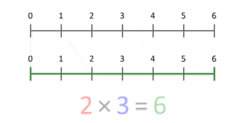
アニメーション的な直観では、ある長さ（スカラー）を別の長さで「スケーリング」する操作とも考えられます。たとえば長さ3の線分を2倍にスケーリングすると長さ6になります（青い点が1から始まり、スケール因子Xの位置で終わるイメージ）。このスケーリングの考え方は、1より小さい数や負の数にも拡張して考えられます。

基本的な性質（数体系ごと）

• 可換性（交換法則）：数の順序を入れ替えても積は変わらない性質。整数や有理数、有理数、その他のすべての実数や複素数において成り立ちます。例：4×6 = 6×4 = 24。
• 結合法則（結合律）：掛け算はグループ化を変えても結果は同じです。例：(2×3)×4 = 2×(3×4) = 24。
• 分配法則：掛け算は加算に関して分配されます。例：2×(3+4) = 2×3 + 2×4 = 14。
• 単位元（1）：1を掛けても元の数は変わりません。例：1×a = a。
• 零との性質：0を掛けると必ず0になります。例：0×a = 0。
• 逆元（除算）：0でない数aには逆数1/aが存在し、a×(1/a) = 1となります（これが掛け算と除算の関係）。

可換でない場合（注意点）

一方で、すべての数学的対象で乗算が可換であるわけではありません。たとえば四元数やベクトルや行列などの演算では順序によって結果が変わることがあり、可換性は成り立ちません。元の文では次のように触れられています：四元数（四次元空間の環として表現可能な数）、ベクトル、行列については、この限りではない。

符号と有理数・複素数での例

• 負の数：(-2)×3 = -6、(-2)×(-3) = 6（負×負＝正）。
• 分数：\(\tfrac{1}{2}×\tfrac{3}{4}=\tfrac{3}{8}\)。分数同士の掛け算は分子同士、分母同士を掛けます。
• 複素数：複素数の掛け算は大きさ（絶対値）を掛け、偏角（回転角）を足すという幾何学的解釈ができます。例：複素数の掛け算は平面上の拡大縮小と回転の組合せです。

記法と表現

• 一般的な記号：×（掛け算記号）、·（中点）、괄弧による省略（例えば2(a+b)は2×(a+b)の意味）や、プログラミングでは*を使うことが多いです。
• 変数同士の掛け算では記号を省略して「ab」のように表すことが多いです。累乗は同じ数を繰り返し掛ける操作（a^n = a×a×...×a）です。

具体例

• 3×5 = 5+5+5 = 15（または3+3+3+3+3 = 15）。この繰り返しの加算という見方は自然数に対して特に直感的です（ここでの「足したもの」は元の説明と同様に足したものという表現で示されます）。
• 分配法則の例：3×(4+2) = 3×4 + 3×2 = 12 + 6 = 18。
• 実数の面積として：幅3、高さ5の長方形の面積は3×5 = 15（単位^2）。

数学的・代数的な文脈では、掛け合わせたい2つの数をまとめて「係数」と呼ぶこともあります。元の表現では数学者は、掛け合わせたい2つの数を一緒に「係数」と呼んだり…といった説明で触れられています（用語としては被乗数・乗数という呼び方が一般的です）。

計算の順序と関連（補足）

算術計算では、乗算は加算より優先して行われます（かっこがない限り）。演算の順序（優先順位）を守ることで式の評価が一意に定まります。掛け算の逆の操作は除算（割り算）であり、元の文にもあるように掛け算の反対は割り算です。

まとめ

乗算は数を組み合わせて新しい量を作る基本的な演算であり、繰り返しの加算、長方形の面積、スケーリングなど多様な直観的解釈があります。整数・有理数・実数・複素数の世界では可換であり、結合律や分配律といった便利な性質が成り立ちますが、四元数・ベクトル・行列などの代数系では可換性が失われる点に注意が必要です。乗算の性質を理解することは、代数や幾何、解析へ進む上での重要な基礎となります。

質問と回答

Q:掛け算とは何ですか?

Q:掛け合わせる2つの数は何と呼ばれていますか?

Q:掛け算は可換なのか?

Q:基数の掛け算はどのように解釈すればいいのでしょうか?

Q:3の5倍はどのように表現するのですか?

Q:掛け算の反対語は何ですか?

文字で検索