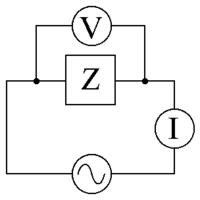
電気インピーダンスとは|複素表示・周波数依存・反射の基礎
電気インピーダンスの基礎を図解で分かりやすく解説。複素表示・周波数依存・反射係数まで、初心者から実務者まで使える実践ガイド。
電気インピーダンスとは、回路が電流や電圧の変化に対抗する量のことです。
インピーダンスの書き方は、主に2つあります。第2図「複素インピーダンス平面」参照
- 抵抗"R"(実部)とリアクタンス"X"(虚部)で、例えば、Z = 1 + 1 j {displaystyle Z=1+1j}のように
- 大きさと位相を持って。
)、例えば Z = 1.4 ∠ 45 ∘ {\displaystyle Z=1.4\angle 45^{\circ }}}のように。
(45度で1.4Ω)
インピーダンスと抵抗はかなり似ています。
抵抗の場合、抵抗器はそれを通過するあらゆる電流に抵抗します。抵抗値が高ければ高いほど、与えられた電流を実現するために必要な電圧が高くなります。式になります。
V = R ∗ I {displaystyle V=R*I}
インピーダンスの場合、インダクタは電流に対して抵抗が変化し、コンデンサは電圧に対して抵抗が変化する。
抵抗とインピーダンスの重要な違いは「変化」という言葉で、変化の速度がインピーダンスに影響を与えます。通常、"変化"は周波数で表され、電流や電圧の方向が変わる毎秒の回数である。式で表されます。
インダクタの場合Z = j 2π f L {displaystyle Z=j2π f L\,}
コンデンサの場合Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2}
ここで、Zはインピーダンスを表す記号、jは虚数-1 {\displaystyle {\sqrt {-1}}}である。

上の式で示されるように、インピーダンスは周波数に応じて変化し、例えば、ゼロヘルツ(DC)では、インダクタのインピーダンスはゼロであり、短絡と同じであり、コンデンサのインピーダンスは無限であり、開回路と同じである。ほとんどの信号は、さまざまな周波数での多数の正弦波の和であり(詳細はフーリエ変換を参照)、それぞれが異なるインピーダンスを経験する。
抵抗と同様に、インピーダンスが高いほど、所定の電流を流すために必要な電圧が高くなります。式は次のようになります。
V = Z ∗ I {displaystyle V=Z*I}
物理的なレベルでは、多くのことを単純化する。
- 抵抗は、抵抗器内の原子と電子が衝突することで発生します。
- コンデンサのインピーダンスは、電界の生成によって引き起こされます。
- インダクタのインピーダンスは、磁場の発生によって引き起こされます。
抵抗とインピーダンスの重要な違いの一つは、抵抗はエネルギーを放散し、それは熱くなるが、インダクタとコンデンサはエネルギーを蓄え、それがダウンしたときに、そのエネルギーをソースに戻すことができるということである。
ソース、ケーブル、負荷のインピーダンスがすべて等しくない場合、信号の一部がソースに反射され、電力を浪費し、干渉を引き起こします。反射の割合は、次のようにして計算できます。
Γ = Z L - Z S Z L + Z S {displaystyle Γ ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}} ここで


波を持つことのできるどんな媒体でも 波のインピーダンスを持っていて 空の空間(光は 電磁波なので 空間を移動することができる)でも インピーダンスは 約377Ω。
補足と分かりやすい解説
複素表示の意味(矩形・極形式)
インピーダンスZは一般に複素数で表され、矩形表示なら Z = R + jX のように実部R(抵抗)と虚部X(リアクタンス)で示します。極形式(大きさと位相)では、|Z|∠θ と書き、|Z| は大きさ、θ は位相角です(例:1.4∠45°)。矩形表示と極表示は互いに変換できます:|Z| = sqrt(R^2 + X^2)、θ = atan2(X, R)。
インダクタとコンデンサのインピーダンス(正しい式)
周波数f(単位Hz)に対する理想素子のインピーダンスは次の通りです。
- インダクタ:Z_L = j ω L = j 2π f L(虚数正の側)
- コンデンサ:Z_C = 1 / (j ω C) = -j / (ω C)(周波数が増すと小さくなる)
ここで ω = 2π f(角周波数)、j は虚数単位(j^2 = -1)です。これらは上の図の式と対応します(ページ内の画像を参照してください)。
DC(0 Hz)での振る舞い
- f = 0 のとき、Z_L = 0(理想インダクタは短絡)となり、直流ではインダクタは電流を自由に流します(ただし実際の巻線抵抗は存在します)。
- f = 0 のとき、Z_C → ∞(理想コンデンサは開放)となり、直流は流れません(充電した後は電流が止まる)。
電力と位相(実効・無効電力)
複素インピーダンスを持つ回路では、電力も複素数で表されます。複素電力 S = P + jQ(単位VA)で、P が実効電力(消費・放散される電力)、Q が無効電力(エネルギーの周期的な蓄積・放出)です。電力因数(power factor)は cos(θ_v - θ_i) のように位相差に依存します。インダクタは電流が電圧より90°遅れ、コンデンサは電流が電圧より90°進む、という基本を押さえてください。
反射、整合、最大電力伝達
伝送線路やアンテナなどで、ソースインピーダンス Z_S と負荷インピーダンス Z_L が一致しないと反射が生じます。反射係数 Γ は
Γ = (Z_L - Z_S) / (Z_L + Z_S)
で与えられ、その絶対値が1に近いほど反射が大きく、0なら完全整合(反射なし)です。最大電力を負荷に渡すためには、ソースの複素共役(Z_L = Z_S*)に一致させる「複素共役整合」が必要な場合があります(特に交流でリアクタンスが存在する場合)。VSWR(電圧定在波比)やスミスチャートは整合設計に便利です。
実装上の注意点
- 実素子は理想から外れ、巻線抵抗や損失、寄生容量・寄生インダクタンスがあります。周波数が高くなるとこれらの影響が顕著になります。
- 複数の素子を直列・並列に組むときは、複素数として和や逆数で計算します。並列インピーダンスの合成は 1/Z_total = Σ (1/Z_k) です。
- 高周波回路では配線の寄生、基板の特性、伝送線路の特性インピーダンス(例:50Ωなど)を考慮する必要があります。
まとめ(要点)
- インピーダンスは抵抗とリアクタンスを合わせた複素量で、周波数に依存します。
- インダクタ:Z_L = jωL、コンデンサ:Z_C = 1/(jωC)。DCではインダクタは短絡、コンデンサは開放です(理想素子の場合)。
- インピーダンスの大きさと位相で電圧・電流の関係を表し、複素電力(P + jQ)でエネルギーの流れを理解します。
- 伝送系ではインピーダンス整合が重要で、整合が取れていないと反射・損失が発生します(Γ を参照)。
さらに詳しい導出や応用(スミスチャートの使い方、複素共役整合、伝送線路理論など)を学ぶと、実際の回路設計や高周波・通信の問題で役立ちます。

複素インピーダンス平面のグラフ表示
♪A AC supply applying the voltage V V ♪ ♪A AC supply applying voltage V ♪ ♪A AC supply applying voltage V ♪A AC supply applying voltage V ♪A AC supply applying voltage V ♪A AC supply apply the voltage V
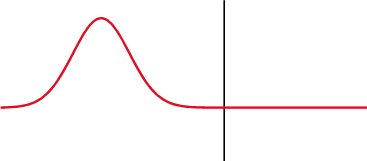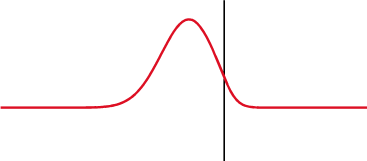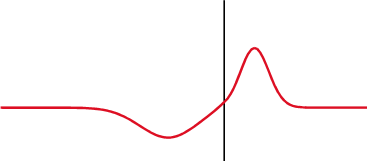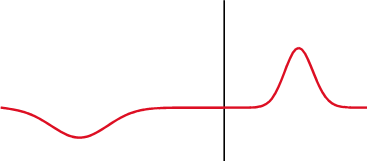
インピーダンスが変化したところで信号が一部反射して戻ってきます。
フェーズ
抵抗器を介して、電圧と電流が同時に上下すると、それらは位相があると言われていますが、インピーダンスではそれは異なり、電圧は、コンデンサでは電流の後ろに1/4波長、インダクタでは前方にシフトされています。
1/4波長は通常、虚数「j」で表されますが、これも90度のシフトに相当します。
虚数"j"を使用することで数学が非常に簡単になり、抵抗器の場合と同じようにインピーダンスの合計を計算することができる。
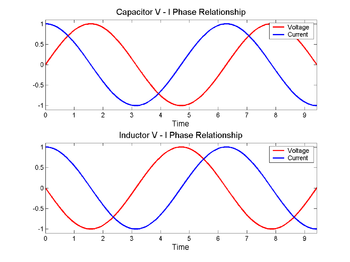
コンデンサ(上)を渡ると、電流(青)の後に電圧(赤)が変化し、インダクタ(下)を渡ると前になります。電圧と電流の位相差は1/4波長です。
質問と回答
Q:電気インピーダンスとは何ですか?
A:電気インピーダンスとは、回路が電流や電圧の変化に対して示す抵抗の大きさです。
Q:電気インピーダンスはどのように書けばよいのか?
A:電気インピーダンスは、抵抗R(実部)、リアクタンスX(虚部)、および、大きさ、位相、サイズ、角度で表記することができる。
Q:抵抗とインピーダンスの違いは何ですか?
A: 抵抗とインピーダンスの決定的な違いは「変化」という言葉であり、言い換えれば、変化の割合がインピーダンスに影響を与える。抵抗は電流が流れても抵抗するが、インダクタは電流の変化に、コンデンサは電圧の変化に抵抗する。
Q: 抵抗とインピーダンスに関連する公式にはどのようなものがあるか?
A:抵抗はV=R*I、Vは電圧、Rは抵抗、Iは電流、インダクタはZ=j2πfL、コンデンサはZ=1/j2πfC、ここでZはインピーダンス、jは虚数-1、πは定数π、fは周波数、Lはインダクタンス、Cはコンデンサを表しています。
Q:抵抗とインピーダンスの物理的な説明にはどのようなものがあるか?
A:抵抗は抵抗器内部で電子と原子が衝突して発生し、インダクタのインピーダンスは電界を、コンデンサは磁界を発生させることで発生する。また、抵抗器はエネルギーを散逸させますが、インダクタとコンデンサはエネルギーを蓄積し、それが低下したときに元の状態に戻すことができます。
Q: 反射率はどのように計算するのですか?
A: 反射係数はΓ=(ZL-ZS)/(ZL+ZS)で計算できます。Γは反射係数、ZSは信号源のインピーダンス、ZLは負荷のインピーダンスを表し、Γ=(ZL-ZS)/(ZL+ZS)で計算できます。
百科事典を検索する