初等代数とは：定義・基本概念・方程式の解法と応用

初等代数の定義・基本概念、方程式の解法から実生活や理系への応用まで図解でわかる入門ガイド

著者: Leandro Alegsa

初等代数は、学生に教える代数学の最も基本的な形式です。多くの場合、算数の次に教える数学の分野の一つで、算数で学ぶ四則演算（＋、−、×、÷）や数の扱いを一般化し、変数（a、x、yなど）を用いて数や関係を表現する方法を学びます。変数を用いることで、より抽象的に問題を扱えるようになり、さまざまな問題のモデル化や解法が可能になります。

初等代数の主要な三つの柱

  • 未知の数（変数）に関する問題を解く能力。これは、方程式とその解法を学ぶことを意味します。例えば、ある数xについて次の式を満たすxを求める問題があります。{\displaystyle 3x+1=10}（この場合は両辺から1を引き、3で割ってx=3と求めます。）
  • 算術のルールを一般化して理解すること。例えば加法の順序を変えても結果が変わらない性質は算数で経験しますが、代数ではそれを記号（変数や式）を使って一般的な法則として扱います。次のような等式や法則を学びます：結合法則、交換法則、分配法則など。例として {\displaystyle 3+4=4+3} のような直感的な等式を、任意の数に対して成り立つ一般的な法則へと拡張します。これにより、具体例から抽象的な思考へ移行する訓練になります。
  • 変数を使って関係（しばしば原因と結果の関係）を表現・解析する力。例えば「チケットを枚売ると利益は 3x − 10 ドルになる」といった関係式を作り、与えられた条件で利益が正になる販売枚数を調べるなどの活用ができます。式の例：{\displaystyle 3x-10}。関数的な見方は、グラフ化して傾向を読み取ることや、変数の変更に対する出力の変化を調べるのに有用です。機能的な（関数の）関係はここで重要になります。

基本概念と用語

  • 式（expression）：数や変数、演算子を組み合わせたもの。例：2x + 5、x^2 − 3x + 2 など。
  • 方程式（equation）：等号で結ばれた二つの式。未知数の値を求めるために解きます（例：3x + 1 = 10）。
  • 項と係数：式は項の和で表され、各項には係数（変数にかかる数）が付きます。例：4x^2 は「項」、4 は係数です。
  • 多項式と因数分解：多項式の展開や因数分解（因数に分ける操作）は方程式の解法やグラフ解析で重要です。
  • 不等式と範囲：不等号を含む式（>、<、≥、≤）の解法や、解の範囲を求める方法を学びます。
  • 関数とグラフ：変数間の対応関係を関数として表し、座標平面にグラフ化して視覚的に理解します。

方程式の代表的な解法

  • 一次方程式（線形方程式）：ax + b = c のような方程式は、移項と割り算で解きます。例：3x + 1 = 10 → x = 3。
  • 連立方程式：複数の一次方程式を同時に満たす解を求める方法として代入法、加減法、行列や行列式を使う方法があります。初等代数では代入法・加減法が基本です。
  • 二次方程式：ax^2 + bx + c = 0。因数分解できれば因数分解で、できない場合は平方完成や二次方程式の解の公式（\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}）を使います。
  • 不等式の解法：不等式は等式と同様に整理しますが、両辺を負の数で掛ける・割ると不等号の向きが反転する点に注意します。区間表現や数直線で解を表すことが多いです。

実世界での応用例

初等代数は理科、経済、工学、建築、コンピュータサイエンスなど多くの分野で基礎として使われます。具体例：

  • 予算や収益のモデル化（収入・費用を変数で表し、利益や損益分岐点を求める）。
  • 物理の基礎計算（速さ・距離・時間の関係、比例・反比例の扱い）。
  • 図形の面積・体積の公式を変数で表して条件に合わせた最適化を行う。
  • データの単純な回帰や傾向分析で直線モデル（y = mx + b）を用いる。

次に学ぶこと

初等代数を習得すると、より高度な分野へ進む基礎ができます。例えば多項式の理論や群・環・体などを扱う抽象代数は大学で学ぶことが多く、初等代数で培った記号的操作や抽象化の力が役に立ちます。また、関数のより厳密な扱いや解析（微分・積分）への橋渡しにもなります。

まとめると、初等代数は変数を用いて問題を一般化・抽象化し、方程式や関数を通じて現実世界の関係を表現・解析するための基礎的な道具です。学校で学ぶ基本的な概念と解法をしっかり身につけることで、科学的思考や問題解決能力が大きく伸びます。

簡単な代数問題

方程式の中に未知の数が1つだけある場合は、簡単に解けることがあります。この未知数を「x」と呼びます。

2 x + 4 = 12.♪♪ {\displaystyle 2x+4=12.\,}

1つの未知の量を持つ簡単な方程式を解くには、未知の量xを方程式の片側に置くために、方程式の両側を同じ数で足し算、引き算、掛け算、または割り算します。x が片方の面に収まったら、算術を使ってもう片方の面の量を決定します。例えば、上の式の両側から4を引くことによって。

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4=12-4} {\displaystyle 2x+4-4=12-4\,}

得ることができます。

2 x = 8 {displaystyle 2x=8,} 2 x = 8 {displaystyle 2x=8,}。 {\displaystyle 2x=8\,}

両辺を2で割る。

2 x 2 = 8 2 2 {displaystyle {\frac {2x}{2}}={\frac {8}{2}}, }。 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}\,}

得ることができます。

x = 4.♪displaystyle x=4. {\displaystyle x=4.\,}

この方程式をシーソーやバランスのように考えるのに役立つかもしれません。

定義

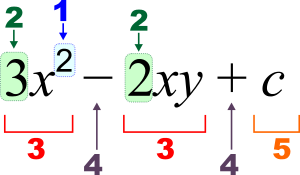
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c{\displaystyle 3x^{2}-2xy+c}}は次の構成要素を持つ。

 

1：指数（乗）、2：係数、3：項、4：演算子、5：定数、x , y {displaystyle x,y}：{\displaystyle x,y}変数

Zoom


質問と回答

Q:初等代数学とは何ですか?


A:初等代数学は学生に教える代数の最も基本的な形式です。通常、算数の後に続き、方程式の中で数字を表す変数（a、x、yなど）を使用します。

Q:初等代数はどのような用途に使われるのか?


A:初等代数は未知数に関する問題の解決，算術の規則の一般化，関数関係の理解と作成，そして科学，ビジネス，建築など他の多くの科目でよく使われます。

Q:初等代数学はどのように抽象的な考えを理解するのに役立つのですか?


A:初等代数はすべてのaとbについてa+b=b+aであることを証明することにより，多くの例から一般的な考え方を学ぶのに役立ちます。

Q:抽象代数は初等代数より高度なのか?


A:はい，抽象的な代数は一般に大学の後半で教えられ，初等的な代数よりもずっと高度なものです．

Q: 初等代数はどのような種類の方程式を扱いますか?


A: 初等代数では変数（a, x, yなど）が数字を表し、演算子（+, -, ×, ÷など）がある方程式が扱われます。
3x+1=10 {displaystyle 3x+1=10｝

Q: 初等代数を理解することは、他の教科にどのように役立つのか?


A: 初等代数を理解することは科学、ビジネス、建築など他の科目にも役立ちます。未知数に関する問題を解決し、異なる変数間の関数関係を作成することができるからです。


百科事典を検索する
AlegsaOnline.com - 2020 / 2025 - License CC3