代数学とは：語源・定義・基本概念と方程式・関数の応用
代数学（Algebra、アラビア語: الجبر、直訳すると"al-jabr"、「壊れた部分の再会」という意味）は、数学の一部である（米国では数学、英国では数学または数字学と呼ばれることが多い）。これは、まだ知られていない値を表すために変数を使用します。等号(=)が使用されている場合、これは方程式と呼ばれます。変数を使った非常に簡単な方程式は次のとおりです：2 + 3 = x。この例では、x = 5、または「xは5に等しい」とも言えます。これをxの解といいます。
方程式の他に、不等式（より小さいものとより大きいもの）があります。方程式の特殊なタイプは関数と呼ばれています。これは、常に1つの入力を1つの出力に変換するので、グラフを作るときによく使われます。
代数学のルールが実生活で機能し、数を使って実物の値を表すことができるので、実際の問題を解決するために代数学を使うことができます。物理学、工学、コンピュータプログラミングは、代数学を常に使用する分野です。また、測量や建設、ビジネス、特に会計などで知っておくと便利です。
代数学をする人は、数のルールや数に使われる数学的な操作を使います。最も簡単なものは、足し算、引き算、掛け算、割り算です。より高度な演算は、平方根や平方根から始まる指数を含む。
代数学は、方程式や不等式を解くために最初に使われました。一次方程式（直線の方程式、y=mx+b）と、二乗（自分自身に掛けたもの、例えば2*2、3*3、x*xなど）の変数を持つ二次方程式の2つが例として挙げられます。
語源と歴史の一部
「代数学（Algebra）」という言葉は、アラビア語のالجبر（al-jabr）に由来し、「壊れたものをつなぎ合わせる」などの意味が含まれます。これは9世紀の数学者、ムハンマド・イブン・ムーサー・アル＝フワーリズミー（アルゴリズムの語源にも関係）らの著作に端を発するとされ、未知数を扱い方程式を解く技術として発展しました。
基本的な定義と用語
- 変数：まだ定まっていない値を表す記号（例：x, y）。元の文中のように変数を使って表現します。
- 方程式：等号(=)を含む式。例：2 + 3 = x。方程式の「解」は、等式を成立させる変数の値です。
- 不等式：大小関係を表す式（<、＞、≤、≥）。元の文で挙げたように不等式は大小を扱います。
- 関数：入力と出力の対応関係。各入力に対して一つの出力が決まるとき、関数と呼び、グラフ化して理解することが多いです（例：y = f(x)）。
- 多項式：項を足し合わせた式（例：ax^2 + bx + c）。二次式は二次方程式につながります。
代表的な演算と操作
基本の四則演算（足し算、引き算、掛け算、割り算）に加え、代数学では以下の操作が頻繁に使われます。
- 指数（累乗）とその計算：例 x^2, x^3。
- 平方根や根号を使った計算。
- 因数分解（例えば ax^2 + bx + c を (mx + n)(px + q) に分ける）や展開（FOIL）
- 式の整理（同類項の整理、展開と因数分解など）
方程式の例と解き方の概要
一次方程式（例：y = mx + b の形）は直線の式です。未知数が1次で表される方程式は、移項・両辺の同じ数での除算などで簡単に解けます。例：
例：2x + 3 = 11 → 2x = 8 → x = 4
二次方程式（ax^2 + bx + c = 0）は、因数分解、平方完成、または二次方程式の公式（解の公式）を使って解きます。代表的な公式：
x = (-b ± √(b^2 - 4ac)) / (2a)
判別式 D = b^2 - 4ac により、解の個数や実数解の有無がわかります（D > 0：異なる2解、D = 0：重解、D < 0：実数解なし）。
関数とグラフ
関数は入力（独立変数）と出力（従属変数）の対応を表します。一次関数（直線）は傾きと切片で特徴づけられ、二次関数は放物線になります。グラフを描くことで、増減や極値、交点（方程式の解に対応することが多い）を視覚的に理解できます。
応用例（実生活と他分野への影響）
- 物理学：運動方程式や力学で未知量を求める際に代数は必須です。
- 工学：設計・解析で模型化し方程式を解く必要があります。
- コンピュータプログラミングは、代数学を使う分野です：アルゴリズム設計や数値計算、データ解析など。
- 測量や建設、ビジネス（例：利率計算や費用の最適化）など、日常的な問題解決にも使われます。
学習のコツと進む順序
- まずは四則演算と正負の数の理解を固める。
- 次に一次方程式、比例・反比例、関数（y = mx + b など）を学ぶ。
- その後、二次方程式、因数分解、平方完成、グラフ化を学び、式の操作に慣れる。
- 問題を多く解いて、式の立て方（現実問題の数式化）を身につけることが重要です。
以上の内容は入門としての概要です。興味があれば、方程式の解法の詳細、抽象代数学（群、環、体など）の概説、数値解法や線形代数（行列と連立方程式）といった次のステップに進むことをおすすめします。
歴史
代数学の初期の形式は、バビロニア人やアレキサンドリアの英雄のようなギリシャの幾何学者によって開発されました。しかし、「代数」という言葉はアラビア語のAl-Jabr（「鋳造」）のラテン語形であり、9世紀にウズベキスタンのクワリズムで生まれたペルシャ人の数学者ムハンマド・イブン・ムサール（Muhammad ibn Mūsā al-Khwārizmī）によって書かれた数学書Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah（「鋳造と方程式の計算に関するエッセイ」）に由来しています。彼はイラクのバグダードのアル・マウンのもとで西暦813年から833年まで栄え、西暦840年頃に死去した。この本はヨーロッパに持ち込まれ、12世紀にラテン語に翻訳された。その後、この本には「代数学」という名前が与えられた。(数学者の名前であるアル・クワリズミの語尾は、ラテン語で言いやすい言葉に変えられ、英単語のアルゴリズムとなった)。
例としては、以下のようなものがあります。
代数の問題の簡単な例を紹介します。
スーは12個のキャンディーを持っていて、アンは24個のキャンディーを持っています。彼らは同じ数のキャンディーを持っているように共有することにしました。それぞれ何個のキャンディーを持っているでしょうか？
以上が問題解決のためのステップです。
- 同じ数のキャンディをもらうためには，アンはスーにいくつかのキャンディをあげなければならない．x はアンがスーにあげるキャンディーの数を表しているとしよう。
- スーのキャンディーに x を加えたものは，アンのキャンディーから x を引いたものと同じでなければならない．12 + x = 24 - x
- 等式の両側から12を引く。これは次のようになります: x = 12 - x. (等号の片側で起こっていることは、方程式がまだ真であるために、他の側でも起こらなければなりません。だから、このケースでは、12が両側から引かれたとき、12 + x - 12 = 24 - x - 12の中間のステップがありました。これに慣れた人は、中間のステップを書き留めないようにしています)。
- 式の両側に x を足します。これは次のようになります：2x = 12
- 方程式の両辺を2で割ると、x = 6となります。答えは6です。アンがスーに6個のキャンディーを与えると、2人のキャンディーの数は同じになります。
- これを確認するために、xがあったところで6を元の式に戻してみましょう：12 + 6 = 24 - 6
- これで18=18となります。これで彼らはそれぞれ18個のキャンディーを持っていることになります。
練習すれば、他の方法では難しい問題に直面したときに代数を使うことができます。高速道路の建設、携帯電話の設計、病気の治療法の発見など、すべての問題に代数学が必要です。
代数の書き方
数学のほとんどの部分と同様に、y（またはy plus z）にzを足すとy + zと書きます。
代数学では、yにzをかける（またはyにzをかける）ことは、y × z、y * z、y-z、または単にyzの4つの方法で書くことができます。掛け算記号の「×」は、変数としてよく使われる「x」に似すぎているので、通常は使わない。また、より大きな式を乗算する場合は、括弧を使用することができます： y (z+1)。
代数学で数字と文字を掛け合わせるとき、文字の前に数字を書きます。5 × y = 5y と書きます。数字が1の場合は、1の倍はどんな数字でもその数字（1 × y = y）なので、1は書かない。
余談ですが、代数ではxやyという文字を使う必要はありません。変数は未知の数値や値を意味する記号なので、どのような変数を使っても構いません。
関数とグラフ
代数学の重要な部分は関数の研究です。関数とは、ある数（または数）を入れて、ある数（または数）を出すことができる機械のようなものです。関数を使う場合、グラフは方程式の解を調べるのに役立つ強力なツールとなります。
グラフは、方程式や不等式を真にする変数のすべての値を示す図です。通常、変数が1つか2つしかない場合には、これを作るのは簡単です。グラフは多くの場合、直線であり、直線が上下に曲がったり、まっすぐになったりしない場合は、基本的な式 y = mx + b で記述することができます。この式はグラフの座標に適用され、線上の各点は(x, y)と書かれています。
線の方程式のような数学の問題では、複数の変数（この場合はxとy）が存在することがあります。線上の点を見つけるために、1つの変数が変更されます。変更された変数を「独立」変数と呼びます。次に、数を作るための計算を行います。作られた数を「従属」変数と呼びます。たいていの場合、独立変数はxと書き、従属変数はyと書き、例えばy = 3x + 1のようになります。これは、x軸（左右に行く）とy軸（上下に行く）を使って、しばしばグラフ上に置かれます。また、f(x) = 3x + 1という関数形式で書くこともできます。ですから、この例では、xに5を入れるとy = 16となります。xに2を入れるとy=7になります。xに0を入れるとy=1になります。したがって，右のグラフのように，点(5,16), (2,7), (0,1)を通る線があることになる。
xが1の乗であれば直線です。2乗やその他の乗の場合は曲線になります。不等式 (< または > ) を使用している場合、通常はグラフの一部が斜線になっており、線の上か下のどちらかになります。
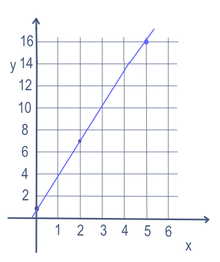
y=3x+1の一次方程式
代数のルール
代数学では、方程式をさらに理解するためのルールがいくつかあります。これらは代数学の規則と呼ばれている．これらの規則は無意味で明白に見えるかもしれませんが、これらの性質は数学のすべての枝に当てはまるわけではないことを理解しておくのが賢明です。したがって，これらの公理的な規則がどのように宣言されているかを知っておくことは，当然のことと考える前に有用である．規則に進む前に，与えられた2つの定義について考えてみましょう．
- Opposite - the opposite of a {a {a} of a {a}
is - a {a {a {a
} . - Reciprocal - reciprocal of a {\displaystyle a} is 1 a {\displaystyle {\frac {1}{a}}}}。
.
ルール
加法の可換性
可換的」とは、関数が数値を入れ替えても同じ結果になることを意味します。つまり、式の中の項の順番は関係ないのです。2つの項の演算子が加算である場合、「加算の可換性」が適用されます。代数的には、a + b = b + a {\displaystyle a+b=b+a
} となる。
これは、引き算には適用されないことに注意してください!(i.e.e. a - b ≠ b - a {displaystyle a-b-bneq b-a} )
乗算の可換性
つの項の演算子が乗算であるとき、「乗算の可換的性質」が適用される。代数的には、a ⋅b = b ⋅a {displaystyle a\cdot b=bcdot a} .
これは除算には適用されないことに注意してください(i.e.e. a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}}} {\frac {b}{a}}}} {\frac {b}{a}}}}}♪ 
when a ≠ b {displaystyle a\neq b} ) )
追加の連想財産
連想」とは、数のグループ化を意味します。足し算の連想性は、3つ以上の項を足し算するとき、これらの項がどのようにグループ化されているかは問題ではないということを意味している。代数的には、a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c}
となります。これは、減算の場合には保持されないことに注意してください。例えば、1 = 0 - ( 0 - 1 )≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1
} （分布性の性質を参照）。
掛け算の連想特性
掛け算の連想性とは、３つ以上の項を掛け合わせるときには、その項がどのようにグループ化されていても構わないということです。ただし、これは除算には当てはまらないので、例えば、２＝１／（１／２）≠（１／１）／２＝１／２ {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2
} .
分配財産
分布的性質は、ある数の掛け算が別の項で分散することができることを示す。例えば： a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} .(
連想の性質と混同しないでくださいね。
加法的同一性特性
同一性」とは、数が自分自身と等しいという性質のことである。言い換えれば、和の変数に等しくなるように、二つの数の演算が存在することである。加法的同一性特性は、任意の数と0の和がその数であることを示している：a + 0 = a {\displaystyle a+0=a
} .これは引き算にも当てはまる： a - 0 = a { {displaystyle a-0=a
} .
乗算的同一性特性
乗算的同一性特性は、任意の数と１の積がその数であることを示している： a ⋅ 1 = a {\displaystyle acdot 1=a
} .これは，除算の場合も保持する： a 1 = a {\displaystyle {\frac {a}{1}}=a
} .
加法逆特性
加法逆特性は、加法同一性特性の反対のようなものである。ある演算が数とその逆数の和であり、それが0に等しい場合、その演算は有効な代数的演算である。代数的には、次のようになる。1の加法逆数は(-1)である。
逓倍逆性
乗算逆特性とは、ある演算が数とその逆数の積であり、それが1に等しい場合、その演算は有効な代数的演算であることを意味する。代数的には、次のようになる。2の乗算逆数は1/2である。
高度な代数
初等代数」、つまり基礎代数に加えて、抽象代数、線形代数、普遍代数など、大学で教えられている高度な代数があります。これには、行列を使って多くの連立方程式を一度に解く方法が含まれています。抽象代数は、数を超えて、数のグループを使ってより抽象的なものへと進む、方程式の中にあるものの研究です。
多くの数学の問題は物理学や工学に関するものです。これらの物理学の問題の多くでは、時間が変数として使われています。代数学の基本的な考え方を使うことで、数学の問題を最も簡単な形に減らすことができ、難しい問題を簡単に解くことができます。エネルギーは e、力は f、質量は m、加速度は a、光速は c であることがあります。これは f = ma や e=mc^2 のような有名な方程式で使われています（この最後の方程式を作るためには代数を超えた複雑な数学が必要でしたが）。
関連ページ
- 数学のトピック一覧
- 業務の順序
- 放物線
- 計算機代数システム
質問と回答
Q:代数学とは何ですか?
A:代数学は数学の一部で、まだ知られていない値を表すために変数を使用します。
Q:代数学で等号は何を意味するのですか?
A:等号（=）は代数学で方程式を意味する。
Q:代数学で関数とは?
A:代数学における関数は，常に1つの入力を1つの出力に変える特殊なタイプの方程式である．
Q:代数学は実際の問題を解決するためにどのように使われるのですか?
A:代数学は現実の問題を解決するために使うことができる。なぜなら、代数学のルールは現実の生活の中で機能し、数値は現実のものの値を表すために使うことができるからである。物理学、工学、コンピュータ・プログラミングは常に代数を使う分野である。また，測量，建設，ビジネス，特に会計の分野でも知っておくと便利です．
Q:代数学ではどのような操作を数字に対して行うのか?
A:代数学では数の法則と足し算、引き算、掛け算、割り算などの数学的演算を行う。より高度な演算では、二乗や平方根から始まる指数が使われる。
Q:代数学で使われる方程式の例にはどのようなものがあるか?
A:代数で使われる方程式の例として、一次方程式（直線の方程式）、二次方程式（変数の2乗を表す方程式）などがあります。
