四色定理

問題の正確な定式化

直感的には、四色定理は、「平面を地図と呼ばれる連続した領域に分離すると、その領域は、隣接する二つの領域が同じ色を持たないように、最大でも四色で着色することができる」と表現できます。この問題を正しく解くためには，いくつかの点を明らかにする必要がある．第一に、3つ以上の国に属するすべての点は無視されなければならない。第二に、面積が有限で周囲が無限の領域を持つ奇妙な地図は、4色以上の色を必要とすることがあります。

この定理の目的のためには、すべての「国」は単純に接続された地域、または連続した地域でなければならない。現実の世界では、これは真実ではない。米国の一部であるアラスカ、アゼルバイジャンの一部であるナクチバン、ロシアの一部であるカリーニングラードは連続していない。特定の国の領土は同じ色でなければならないので、4色では十分ではないかもしれません。例えば、左図のような簡略化された地図を考えてみましょう。この地図では、Aと表示されている2つの地域は同じ国に属しており、同じ色でなければなりません。この地図では、「A」と表示されている2つの領域は同じ国に属しており、同じ色でなければならないので、この地図には5色の色が必要です。Aの領域が3つしかない場合は、6色以上の色が必要になるかもしれません。このようにして、任意の数の色を必要とする地図を作ることができる。同様の方法は、現実の地図で通常使われるように、すべての水域に単色を使う場合にも当てはまります。

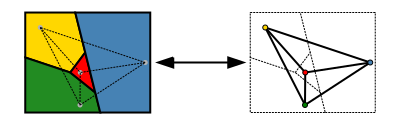
この定理をより簡単に表現するには、グラフ理論を使用します。地図の領域の集合は、より抽象的には、各領域に頂点を持ち、境界線を共有する領域のペアごとに辺を持つ無向グラフとして表現することができる。このグラフは平面グラフである：各頂点を対応する領域内の任意の位置に配置し、各頂点の位置から各領域内の共有境界点まで交差することなく曲線として辺を描くことで、交差することなく平面上に描くことができる。逆に，平面グラフは，このようにして地図から形成することができる．グラフ理論の用語では、４色定理とは、すべての平面グラフの頂点は、隣接する２つの頂点が同じ色を持たないように、最大でも４色で着色できる、つまり、「すべての平面グラフは４色で着色可能である」ということである(Thomas 1998, p. 849; Wilson 2002)。

アゼルバイジャンの非連続地域を含む地図の例


この地図は4色では着色できません

歴史

この問題に最初に名前を挙げたのは1852年のフランシス・ガスリーです。彼は当時イギリスの法学部の学生でした。彼はイングランドの郡の地図を描くためには、少なくとも4色の色が必要であることに気付きました。オーガスタス・デ・モーガンがこの問題について最初に話し合ったのは、1852年8月にローワン・ハムリトンに宛てた手紙の中でのことでした。その手紙の中で、デ・モルガンは、隣り合った国が異なる色になるように、本当に地図を彩るのに4色で十分なのかと問いかけています。

イギリスの数学者アーサー・ケイリーは1878年にロンドンの数学者協会にこの問題を発表した1年以内に、アルフレッド・ケンペは、この問題の証明のように見えるものを発見した。11年後の1890年には、パーシーHeawoodは、アルフレッドの証明が間違っていたことを示した。ピーター・ガスリー・テイトは1880年にもう一つの証明の試みを発表しました。テイトの証明もうまくいかなかったことを示すのに11年かかった。1891年、ジュリアス・ピーターセンはこれを示すことができた。彼がケイリーの証明を改竄したとき、ケンペもまた、彼が五色定理と呼んでいる問題の証明を示した。この定理によれば，このような地図は5色以下の色で着色することができる．そこには2つの制約がある。第一に、どの国も連続していて、エクスクラブがないことです。第二の制約は，国は共通の境界線を持っていなければならないということである．ケンペの証明が間違っていたにもかかわらず、彼は後に正しい証明を可能にするアイデアのいくつかを使用しました。

1960年代と1970年代に、Heinrich Heeschがコンピュータによる証明の最初のスケッチを開発した。Kenneth AppelとWolfgang Hakenは、1976年にこのスケッチを改良した(Robertson et al. 1996)。彼らは、テストする必要があるケースの数を1936個に減らすことができましたが、その後のバージョンでは、1476個のケースのみのテストに頼ったものが作られました。各ケースはコンピュータでテストする必要がありました(Appel & Haken 1977)。

1996年、ニール・ロバートソン、ダニエル・サンダース、ポール・シーモア、ロビン・トーマスは、この方法を改良し、テストするケースの数を663に減らしました。この時も、各ケースをコンピュータでテストする必要がありました。

2005年、ジョルジュ・ゴンティエとベンジャミン・ヴェルナーは正式な証明を開発した。これは、初めて定理証明ソフトウェアを使用することができるようになったため、改良されたものでした。使用したソフトウェアはCoq.

四色定理は、コンピュータの助けを借りて証明された最初の大きな数学的問題である。証明は人間が行うことができないため、一部の数学者は証明が正しいとは認めなかった。証明を検証するためには、正しく動作するソフトウェアやハードウェアに頼らなければならない。また、証明はコンピュータで行われているため、あまりエレガントなものではありません。

間違っていることが判明した試み

四色定理は、その長い歴史の中で、多くの偽証明や反証を引き寄せてきたことで悪名高い。当初、ニューヨーク・タイムズ紙は、アッペル＝ハーケンの証明についての報道を拒否しました。新聞社は、ポリシーの問題としてこれを行ったのである。いくつかの証拠は、偽造できるようになるまでに長い時間がかかった。Kempe の証明と Tait の証明の改ざんには 10 年以上かかった。

最も単純な反例は、一般的に、他のすべての領域に触れる一つの領域を作成しようとします。これにより、残りの領域は 3 色だけで着色されることになります。しかし、地図を描く人は1つの大きな領域に集中しているので、残りの領域が実際には3色で着色できることに気がつきません。

このトリックは一般化できる。地図の中のいくつかの領域の色をあらかじめ決めておくと、残りの領域を全部で4色しか使わないような色付けができなくなります。反例を検証する人は、これらの領域の色を変える必要があるとは考えていないかもしれません。そうすると、反例が有効であるように見えてしまいます。

おそらく、この一般的な誤解の根底にある一つの効果は、色の制限が一過性のものではないという事実です。もしこれが制限であるならば、平面グラフは任意の数の色を必要とするでしょう。

他にも、複数の切断された部分を持つ領域を使用したり、同じ色の領域がある点で接触することを許さなかったりと、予期せぬ方法で定理の仮定に反した誤判定が行われています。

政治地図のぬりえ

現実の生活では、多くの国にはエクスクラブや植民地があります。それらはその国に属しているので、親国と同じ色で着色する必要があります。つまり、通常、このような地図を彩色するためには、4色以上の色が必要となる。数学者がこの問題に関連したグラフについて語るとき，それは平面ではないと言う．グラフが平面であるかどうかは簡単に調べられるが，色をつけるのに必要な色の数が最も少ないグラフを見つけるのは非常に困難である．これはNP完全問題であり，存在する問題の中で最も難しい問題の一つである．グラフを着色するのに必要な色数の最小値は，その色数として知られている．4色定理を解こうとしたときに起こる問題の多くは離散数学に関連している。このため、代数的位相幾何学からの方法がよく用いられる。

フラットでない」マップへの拡張

4色の定理は、「地図」が平面上にあることを必要とします、数学者は平面と呼んでいます。1890年、パーシー・ジョン・ヘアーウッドは、現在ヘアーウッド推論と呼ばれているものを作りました。これは、４色の定理と同じ質問をしていますが、どんなトポロジカルな物体に対しても同じ質問をしています。例えば、トーラスは、最大でも７色で着色することができます。ヘアウッドの推論は，クラインの瓶を除いて，そのようなすべての物体に有効な公式を与えている．