不確定性原理

ダイアグラム

6.このアニメーションは、宇宙の不確実性の性質の重要な結果の一つである電子の量子トンネルを示しています。注意深く見てください。毎回少しずつバリアを通過していきます。


5.中心のギャップをスプリングスケールで吊るすことで運動量を測定できますが、そのためにギャップが予想外に動いてしまい、各光子の位置情報が失われてしまいます。


4.4.小さな穴の開いたバリアをバネで取り付けると、粒子が穴を通過することでバリアが押され、バネが伸びて運動量が測定されます。しかし、バネを取り付けたバリアが動くため、穴を通過したときに粒子がどこにいたのかがわからなくなり、回折の影響で検出画面上の粒子の位置にも影響が出てしまいます。


1.光子や電子などの素粒子は、大きな穴を通って撃たれると鋭いピントが合うようになりますが、途中でどこにあったのかは正確にはわかりません。


2.穴を狭くすると、穴の縁の周りの粒子の通り道が曲がってしまう（回折）ので、結果的にビームが大きくなり、柔らかくなります。


3.穴を狭くすることで、真ん中の位置の確実性は高まりますが、そこから右側の検出画面までの方向が不確かになります。焦点がぼやけてしまいます。穴を広げると、光子はすべて検出画面の中心で終わりますが、中央の障壁を通過したときにどこにいたのかがわからなくなります。

人間はどのようにして不確実性を学んだのか？

ヴェルナー・ハイゼンベルクが新しい量子物理学を作った直後、彼の数学から予期せぬものが出てきました。

ｘΔｘΔｐ ｐ 涙を流してくれる人がいるんだよね。

位置(x)の誤差の範囲と運動量(p)の誤差の範囲は、プランク定数を4πで割った値とほぼ等しいか、それ以上である。

これらの記号は、上の写真ですでに見たことを数学の形にしたものです。この記号は、何かがどこにあるのか、どこに向かっているのかを完全に把握することはできない、ということを明確に示しています。もし、それがどこにあるのかがはっきりしてきたら、それがどこにどのくらいの速さで進んでいるのかについての見当がつきにくくなります。もし、あなたがそれがどこに行っているのか、どのくらいの速さでいつでも明確になれば、あなたはそれが今どこにあるのかについての考えが少なくなります。

科学者たちは、ある物質が加熱されたり励起されたりすると、なぜ光の特徴的な色を発するのかをすでに学んでいました。ハイゼンベルクは、これらの色がそれぞれ特徴的な明るさを持つ理由を説明しようとしていました。ハイゼンベルクや他の科学者たちが「そういうことです」と言っただけでは十分ではなかったでしょう。彼らは、これらの違いには何か理由があるはずだと確信していましたし、輝線の強さの比が元素のサンプルごとに常に同じであることにも納得していました。

各元素に特徴的な色の線の強さの説明を探ろうとしたとき、彼は自然の隠された秘密につまずくことになろうとは思ってもみなかった。量子力学の研究で、水素のスペクトルの中で人間が見える部分に4本の明るい線がある理由はすでにわかっていた。次に学ぶべきことは、その明るさをどうやって計算するか、ということだったに違いありません。水素は電子が1個しかなく、可視領域では4本の線しかないので、水素から始めるのは当然のことのように思えました。同じ明るさではないのには何か理由があるに違いありません。ネオンと他の元素の異なる色の線の明るさの説明は後回しにしました。

 

ハイゼンベルクは、電気の古典的な方程式を応用して量子物理学の研究を始めましたが、それはもともと非常に複雑なもので、1925年の論文の背後にある計算は非常に難しいものでした。

彼は水素ランプのスペクトルの明るい線の強度を計算する正しい方法を見つけようとしていました。彼は、「振幅」と呼ばれる関連する量を見つけ、振幅に振幅を掛け合わせて（言い換えれば、振幅を二乗して）、自分の求める強度を得なければなりませんでした。彼は、水素ランプがすべての周波数で放射しているわけではなく、人が見ることのできるスペクトルの一部では、連続した周波数の範囲で放射しているわけではないという事実を考慮して、振幅を表現する方法を考え出さなければならなかった。ハイゼンベルグは、振幅を計算する驚くべき新しい方法を発見した。

ハイゼンベルクが発見し、ある量子量(例えば位置)を別の量子量(例えば運動量)に乗算するのに使った奇妙な方程式|方程式は、"1925年7月のハイゼンベルクの'魔法の'論文"と呼ばれてきたもので発表されています。

C ( n , n - b ) = ∑a A ( n , n - a ) B ( n - a , n - b ) {displaystyle C(n,n-b)=sum _{a}^{},A(n,n-a)B(n-a,n-b)} } } }

上の計算は非常に難しく見えますが，そこに至るまでの計算は非常に難しく，非常にわかりにくいものです。ここでは、それがどのように見えたかを示すためだけに与えられています。ハイゼンベルクの論文は歴史的なランドマークです。彼の論文を読んだ物理学者の多くは、彼の結論に異論はないが、どのようにしてその結論に至ったのか、彼の説明にはついていけなかったと言っています。ハイゼンベルグが使った始点方程式はフーリエ級数を含み、多くの因子を含んでいました。上の式は、行列の書き出しと掛け算のレシピのようなものだからです。

ハイゼンベルクは電子の軌道のようにあるものがゆっくりと大きくなったり小さくなったりしない奇妙な世界を記述していたので、新しい方程式はとても奇妙で異常なものでなければなりませんでした。新しい種類の変化には、ジャンプとジャンプの間の大きなギャップが含まれています。電子は特定の軌道間をジャンプすることしかできず、軌道間の変化で得られるエネルギーや失われるエネルギーは、正しいエネルギーの光子が吸収されたり、正しいエネルギーの新しい光子が生成されたりしたときに発生します。水素原子の中の電子が2つの特定の軌道の間で最も頻繁にジャンプして降りる（落ちる）ならば、そのエネルギーレベルでより多くの光子が放出されることになり、そのレベルで生成される光が最も強い光になります。

連続スペクトル（太陽の光をプリズムに通したときに見えるもの）のために作られた方程式を、何もない間にいくつかのピーク周波数を持つだけのスペクトルに適合させるのは困難でした。光とエネルギーについて学んできたことは、ほとんどすべて、燃えるロウソクや太陽のような大きな物体を使って行われてきましたが、それらの大きな物体はすべて連続スペクトルを生成します。このような普通の大きさのものは実験が簡単にできても、それを支配する法則（物理法則）を解明するのには、まだ長い時間がかかっていました。今、物理学者たちは、あまりにも小さくて見えないもの、連続スペクトルを出さないものを扱っていて、少なくとも、これらの小さくてギャップのある光源の法則を見つけるのに役立つような、すでに知っていることから手がかりを得る方法を見つけようとしていました。

元々の方程式は、ある種の振動体が波を発生させるもので、臓器のリードが特徴的な周波数の音波を発生させるようなものでした。つまり、（リードの振動のように）前後に運動があり、正弦波としてグラフ化できる放出波がありました。原子レベルの物理学では、それまでわかっていたことの多くは、電子が原子核の周りを移動することに関係していました。質量が軌道上を移動するとき、ある種のハブの周りを回転するとき、それは「角運動量」と呼ばれるものを持っています。角運動量とは、メリーゴーランドのようなものが、人が押すのを止めた後も回転し続けるようなものです。位相計算や角運動量の計算は複雑です。その上、ハイゼンベルクは1925年の論文ですべての計算結果を示していないので、優秀な数学者でも、彼が言わなかったことを埋めるのに苦労することになるかもしれません。

多くの物理学者が、ハイゼンベルクの画期的な論文の様々な数学的ステップを理解できないと言っていたにもかかわらず、最近のある論文では、ハイゼンベルクがどのようにしてその結果を得たのかを説明しようとしているのですが、その論文は数学で埋め尽くされたページを20ページも使っています。その記事でさえ、理解するのは簡単ではありません。数学は非常に難しいものから始まり、最終的にはこの記事の一番上にあるような比較的単純なものができあがってくるのです。単純な結果を得るのは簡単なことではありませんでしたし、時代遅れの宇宙像から新しい量子物理学へと移行する過程を示すつもりはありません。ハイゼンベルクがブレークスルーをしたとたんに、これまで誰も見たことのない宇宙の仕組みの一部が見えてきたことを示すためには、十分な詳細が必要です。

ハイゼンベルクは興奮していたに違いありませんが、とても疲れていたのも事実です。夜遅くになって、彼はついに突破口を開き、それがうまくいくことを自分自身で証明し始めました。ほとんどすぐに、彼は何か奇妙なことに気がついた。しかし、それはこの小さな厄介な問題が大きな発見であることが判明したのです。

ハイゼンベルクは、振幅を振幅で乗算することを目指していたが、今度は彼の新しい方程式を使って振幅を表現する良い方法を手に入れたのである。当然、彼は乗算のことを考えていたし、複雑な方程式で与えられたものをどうやって乗算するかを考えていた。

ハイゼンベルグは、振幅の二乗以外にも、いずれは位置に運動量をかけたり、エネルギーに時間をかけたりしたいと考えていることに気がついた。ハイゼンベルグは、位置に運動量を掛けた場合でも、運動量に位置を掛けた場合でも問題にならないと考えていた。両者が単純な数であれば何の問題もなかっただろう。しかし、どちらも複雑な方程式であり、その方程式にどうやって数字をはめ込むかは、どちらから始めるかによって違ってくることがわかりました。自然界では、位置を測ってから運動量を測るか、運動量を測ってから位置を測らなければなりませんでしたが、数学では同じ一般的な状況が優勢でした。(あなたがうるさい詳細を学びたい場合は、英語版ウィキペディアの記事行列力学へのハイゼンベルクの入り口を参照してください！)結果の間の小さな、しかし厄介な違いは、ハイゼンベルクがどれだけ彼らが去っていくことを願っていたかに関係なく、残っていこうとしていた。

当時、ハイゼンベルクはその小さな問題を片付けることができなかったが、疲労困憊していたため、直属の上司であるマックス・ボーンに仕事を渡して休暇に入った。

マックス・ボーンは注目すべき数学者であったが，すぐにハイゼンベルグが与えた方程式が行列を書くためのレシピのようなものであることに気づいた．ボーン博士は当時，ほとんどの人があまり役に立たないと思っていたこの奇妙な数学に興味を持っていた数少ない人の一人であった．彼は行列は掛け算ができることを知っていたので、ある物理学の問題を計算するためのすべての計算は、ある行列に別の行列を掛け算することで処理できるということを知っていました。複雑な手続きを標準的で許容できる形にすることができれば，それだけで作業が楽になるだろう．また、他の人にも受け入れられやすくなるかもしれません。

ボーンはそのような優れた数学者であったので，2つの行列の乗算の順序を入れ替えると，異なる結果が得られ，その結果はわずかに異なることにすぐに気づくことができた．その差はh/2πiである。日常生活では，その差は目に見えないほど小さいものである．

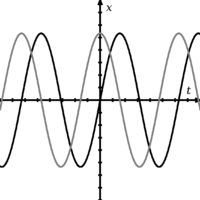
互いに位相がずれている2つの波


ネオンスペクトル


太陽のフルビジュアルスペクトル。隙間はありません。このチャートは、様々な周波数での強度を示しています。


特定の分子が励起されると、その分子は特徴的な色を発します。


水素スペクトル

不確実性の形式論へ

数年かかりましたが、ハイゼンベルグは、Δx × Δp = h/2という不確かさの原理を証明することができました。ハイゼンベルクは、1927年にこの理論を紹介する論文を書いたときに、この以前の結果から不確実性原理を導き出したと説明しています。

hと書かれた定数は、プランク定数と呼ばれていますが、よくある謎の数字なので、この小さな数字が何なのかを理解しておく必要があります。数値的には、通常、6.62607×10^-34 J秒（ジュール秒）で表されます。つまり、エネルギーと時間が関係している量なのです。

完全放射体（黒体放射体と呼ばれる）のエネルギーが、「クアンタ」（この言葉の単数形は「量子」）と呼ばれる決まった大きさの単位で放出されていることにプランクが気付いたことで発見された。放射されたエネルギーは光子として放出され、光子の周波数はそれが与える「パンチ」に比例します。我々は、異なる色として可視光の異なる周波数を経験しています。スペクトルの紫の端では、各光子は比較的大きなエネルギーを持っており、スペクトルの赤の端では、各光子は比較的小さなエネルギーを持っています。光子のエネルギー量を計算する方法は、E = hν（エネルギーはプランク定数の倍の"ν"または周波数に等しい）の式で与えられます。

ハイゼンベルクの不確定性原理Δx × Δp ≥ hは、特定の数のペアを特定しようとするときはいつでも、私たちはそこまで近づくことができ、もし私たちがそのうちの1つについてより明確になろうとするならば、すなわち、私たちが何かの位置についてより良いアイデアを持っているようにΔxを小さくしようとするならば、私たちはペアの他の数のためのより大きな数を手渡されなければならないことを教えてくれています。

もう一つの物理量のペアは、不確実性の関係に従います：ΔE × Δt ≥ hであり、このペアは、他のものの中で、もし我々が星間空間、我々が全く何かを見つけることを期待していないであろう場所を見て、Δtをどんどん0に近づけていくと、式に示されているバランスを保つために、ΔEはますます大きくならなければならないことを示しています - そして突然、その短い期間だけで、運動量のある何かが存在することができます。

この不確定性（確実性の欠如）はどのように説明されるべきなのでしょうか？宇宙では何が起こっているのか？新しい理論が成功した場合、調査中の現象について新しい情報が得られることがあるとよく言われます。ハイゼンベルグは、水素の輝線スペクトルの正しい強度を予測する数学モデルを作ったが、そのつもりはなくても、ある物理量のペアが予想外の不確実性を開示していることを発見した。それまで誰も、測定がより正確で正確なものになることは永遠にありえないという考えを持っていませんでした。測定値をより確実に、より明確にすることができないという事実は、驚くべき新しい発見でした。多くの人がそれを受け入れようとはしなかった。

ボーアとその同僚たちは、光子や電子などは測定されるまで位置や運動量を持たないと主張しました。この理論的立場は、不確実性の発見から生まれたものであり、何を信じるかという個人的な好みだけではありませんでした。ボーアは、光子や電子のようなものは、観測してみないと何もわからないと言いました。このような小さなものを観測するためには、何らかの方法でそれと相互作用する必要があります。おそらく自動車の重さで舗装にある小さなレバーを押し下げて、それぞれのレバーに取り付けられた時計を止め、自動車の重さを記録するのだろう。最終的には、自動車が様々な時間にどこにあったかの明確な記録を持つことになり、また、進行方向と重量を計算することができます。そうすれば、時計を見ればいつでも自動車の位置と運動量（速度に質量を掛けたもの）を知ることができます。小さなレバーを動かすのに必要な力が自動車の進行に影響を与えるとは想像もできないでしょう。また、舗装上のレバーのある地点の間に自動車の位置や軌跡がないことや、その間に自動車が三次元的なモヤモヤの中に存在し、レバーを押している間だけ落ち着くことも想像できないだろう。私たちが見慣れた世界では、このような奇妙な相互作用は見られない。

暗い夜に海の上の船の位置を特定するには、サーチライトを使えば、船の位置や進行方向を妨げることはありませんが、光を使って電子の位置を特定するには、電子の位置や軌道を妨げるのに十分な運動量を持った光子を1個以上ぶつけなければなりません。他の方法で電子の位置を特定するには、ある種の物理的な拘束具で電子を保持しなければならず、それによって電子の前進運動も停止してしまうことになります。

光子の位置を特定するためには、光子の前進を止めずにできる最善の方法は、障壁の円形の穴を通過させることである。レーザーなどで光子が出た時間と、デジタルカメラなどの検出画面に光子が到達した時間が分かれば、その距離を移動するのに必要な時間と、光子が円形の穴を通過した時間を計算することができます。しかし、光子を通過させるためには、円形の穴の直径が光子の大きさよりも大きくなければなりません。円形の穴を小さくすればするほど、その穴を通過する光子の正確な位置を知ることができるようになります。しかし、その時に光子が中心からずれているかどうかはわかりません。穴の大きさが光子の大きさと全く同じであれば、穴を通過することはできません。穴の直径が小さくなればなるほど、光子が穴から出るときの運動量や方向が大きく変化します。

ニールス・ボーアらは、顕微鏡でも見えないような小さすぎるものを、日常生活のスケールでしか証明できないものを、そうだと思い込んでしまうと、大変なことになると主張しました。日常生活の中では、物事は常に一定の位置を持っています。原子のスケールでは、その結論を裏付ける証拠がない。日常生活の中では、物事にはそれが起こる時間が決まっています。原子レベルでは、その結論を裏付ける証拠はない。日常生活の中で、1日目の夜勤から2日目の昼勤まで工場を見ていて、完成した自動車が出荷ドックに運ばれてくるのを見たら、夜勤中に運ばれてきたのか昼勤中に運ばれてきたのかが分からないと言っても意味がありません。しかし、原子スケールでは、1つの光子が2回出たとカウントしなければならない例を示すことができます。それが悪ければ、隣り合った2つのレーザーから1つの光子が出ている例もあります。

原子スケールで何が起こっているのかを知ることの難しさの一つは、何かがどこにあるのか、その軌道はどうなっているのか、その両方を知りたい、同時に両方のことを知りたいと思うのですが、位置と軌道を同時に測定することはできません。光子や電子の運動量を一度に測ってから、必要以上に遅れずにその位置を測るか、あるいは逆に、位置を先に測って運動量を後に測るかのどちらかになります。問題は、最初の測定をかなり明確な形にすることで、次の測定の不確かさを増大させてしまうことです。最初の測定があまりにも粗雑で、それぞれに多くの誤差が発生していた場合は、より軽いタッチでそれぞれの測定を行うことで改善することができますが、精度のある限界を超えることはできません。

私たちは、スピンサイクルで洗濯機の上に置かれた浴室の体重計で何かを量ろうとすると、体重計の針がひどく揺れるので、不正確な結果が得られることを日常生活から知っています。洗濯機の電源を切ることができます。しかし、非常に正確な測定をするためには、近所を通るトラックが針をガタガタさせてしまうので、何かの上に置いて外からの振動を遮断することができます。そのため、何かの上に体重計を置いて外部からの振動を遮断することで、精度の高い測定が可能になると考えています。スケールの上のもの自体が振動していることや、それが不定の運動量を持っていることを考慮することはありません。

不確実性の原理から逆算すると、実際にはどんな原子スケールのものにも明確な位置や明確な運動量は存在せず、実験者は不確実性の原理で示された限界の中でしか物事を明確にすることができないということのようです。ボーアと彼の同僚たちは、測定をしなければ何もわからない、測定が行われたときには、より明確な位置やより明確な運動量の方向に物事を押し出すことはできるが、私たちが望むような絶対的な明確さや確実さを得ることはできない、ということだけを主張しました。しかし、他の人たちはその可能性を真摯に受け止め、もし数学が正しいならば、超小型の世界では絶対的な確実性や確実性はありえないと主張しました。数学は現実のモデルに過ぎず、それが正しいモデルである保証はないというのが科学の本質です。

数学が予測していることの信頼性と実際の結果は、非常に異論を唱えにくいものですが、数学が現実の世界について語っていることは、いくつかの異なる考えを生み出してきました。コペンハーゲンでニールス・ボーアと一緒に働いていた科学者の間では、不確定性原理は、初歩的なレベルでは物理的宇宙は決定論的な形では存在しないということを意味すると考えられていました。むしろ、それは確率や可能性の集合体である。

コペンハーゲングループが数学で織り成す話に反して、量子論によれば、複数の可能性のある結果があるたびに、それぞれの結果はそれぞれの新しい宇宙で発生するという「複数の宇宙解釈」などの話もあります。アインシュタインは、複数の可能性のある結果は存在しないので、宇宙は一つしかなく、それは確定的なものであると主張した。"神はサイコロを振ることはない"

もし h が最小のエネルギー量であれば、様々な周波数の光子に含まれるエネルギーを示す基本的な方程式は均衡しません。それは間違っているだろう。

不確実性の原則に対する異議申し立て

アルバートアインシュタインは、新しい量子力学は、測定が行われている前の時間の位置と運動量の欠如を意味することを見て、彼は強く異議を唱えた。彼はしっかりと物事は、彼らが測定された前に、明確な位置と明確な運動量を持っていたと信じていたし、物事のペアのいずれかを測定し、正確に他のものを測定する可能性を乱すという事実は、事前にそれらのいずれかの欠如があることを主張していません。彼と彼の同僚の2人は、"EPR論文"として知られるようになったものを書きました。その論文では、位置と運動量を決定する特性があるはずで、それを見ることができれば、あるいはそれに関する情報を得ることができれば、位置と運動量を数学的に知ることができ、予測することができると主張しています。長い間、人々は何を証明したり、アインシュタインの信仰の記事だった反証する方法がなかったと思った。それはもつれのすべての近代的な開発につながったので、引数は非常に生産的だった。

数学的には、アインシュタインは間違っていることが証明されています。1964年、ジョン・スチュワート・ベルは、それらを調査する2人の個人にとって単に未知の状態である確定的な状態を持つ2つの粒子と、測定されるまで不確定または不確定な状態であるもつれた状態を持つ2つの粒子の振る舞いを区別するための数学的方法を開発しました。彼の方法は、2つの異なる仮定の下では、ある結果が得られる確率が異なることを示しています。彼の研究は、ベルの定理またはベルの不等式と呼ばれています。実験によって、自然はベルが説明するように振る舞うことが示されている。

不確定要素への別ルート

ハイゼンベルクの不確定性原理の初期の議論は、電子や陽子などの物質の粒子が波長を持っていることを考慮しないモデルに依存していた。1926年、ルイ・ドブロイは、光子に限らず、すべてのものには固有の周波数があることを示した。物体にも光子と同じように波動性と粒子性があります。もし、陽子のようなものの波動を狭く高くしようとすると、その位置がはっきりしますが、運動量の定義が悪くなります。もし、波の記述の運動量の部分をより明確にしようとするならば、つまり、より狭い値の範囲内にとどまるようにしようとするならば、波のピークは広がり、その位置はより明確ではなくなってしまいます。

光子の記述の一部である波は、量子力学的には、海の表面にある波や、音波を構成する圧縮空気や希薄空気の領域と同じようなものではありません。その代わりに、これらの波にはピークや高振幅の領域があり、それは空間と時間のその時点で何かを見つける確率に関係しています。より正確には、ある現象が現れる確率を与えるのは、振幅の二乗です。

光子に適用される波は純粋な正弦波かもしれません。その場合、すべてのピークの値の二乗が、その点で光子を観測する確率を与える。正弦波の振幅はどこでも同じなので、それぞれのピークで光子を見つける確率は同じになります。ですから、現実的に言えば、これらの光子の一つの波を知っていても、どこでそれを探せばよいかの手がかりは得られません。一方、光子の運動量は数学的にはその波の振幅に関係しています。この場合、純粋な正弦波があるので、波の各周期の振幅は同じであり、したがって、この波に関連する運動量の値は1つしかありません。光子がどこに当たるかはわかりませんが、どのくらいの強さで当たるかは正確にわかります。

検出スクリーン上のある点に焦点を合わせる光のビームでは、光子に関連する波は純粋な正弦波ではありません。その代わりに、ある点では高い振幅を持ち、その最も高いピークの両側でははるかに低い振幅を持つ波である。数学的には、このような波を、波長の異なるいくつかの異なる正弦波に分析することが可能です。ある周波数の最初の正弦波に、異なる波長の第二の正弦波を加え、第三の正弦波を加え、第四の正弦波を加えることによって、このプロセスの逆を視覚化するのは少し簡単です。その結果、1つの高いピークを持つ複雑な波となり、波長の異なる、したがって運動量の異なる波が多数含まれることになります。この場合、光子がある点に現れる確率は非常に高くなりますが、光子が出す運動量は、構成波のいずれかの波長に関係していることがわかります。言い換えれば、組み立てられた「異なる波長の波」のすべての長さを考慮しなければならないので、p = ħ/λの値はもはや単一の値ではありません。

シミュレーションでは、粒子の位置のシャープアップを数学的にモデル化する方法を示しています。元の正弦波に多くの異なる波形を重ね合わせます。中心部はより高く、より高いピークを形成し、残りのピークは数は増えますが、お互いに干渉するので高さは減少します。だから最終的には、重ね合わせの中に多くの異なる波があり、それぞれが異なる波長と（p = ħ/λによって）異なる運動量を持つが、1つだけの非常に高いピーク、より高く、より狭く成長し、私たちに決定的な位置に近いものを与えてくれるものがあります。

運動量をより明確にするためには、単純な正弦波だけが残るまで、重畳された正弦波をどんどん取り除かなければなりません。そうすることで、中心のピークの高さが徐々に減少し、粒子を見つけることができる競合する場所の高さが徐々に増加していきます。

そのため、素粒子の波動図から始めるときには、通常、比較的背の高い中心ピークと比較的多くの成分波長を持つ場合を扱います。このような状況では、正確な位置や正確な運動量を予測することはできません。もし数学モデルが現実世界を正確に表現しているのであれば、光子や他の素粒子は正確な位置や運動量を持っていません。このような粒子を測定するときには、ピークをさらに絞って狭くする方法を選択することもできますし、ピークを下げて成分の波長を均等にする方法を選択することもできます。何をどのように測定するかによって、位置をより明確にしたり、運動量の範囲を狭くしたりすることができます。いろいろな方法で装置をぐちゃぐちゃにしないように実験を設計することはできますが、そもそも完全に確定したものがなかったという事実は拭えません。

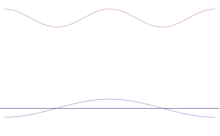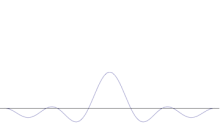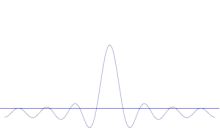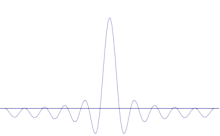
いくつかの平面波の重ね合わせ。波のパケットは、多くの波が加わることで、ますます局在化していく。フーリエ変換は、波束を個々の平面波に分離する数学的操作です。量子力学では波動関数は一般的に複雑であるのに対し、ここで示した波動は説明のためだけに実在するものであることに注意してください。

文化的影響

ハイゼンベルク不確実性原理の最も重要な影響は、意志の自由に関する議論にあります。古典物理学の理論の下では、原因と結果の法則は不変であり、宇宙がある方法で始まったならば、将来発生するすべての物質とエネルギーの相互作用は、その初期状態から計算できると主張することができます。すべてのものは、その前に来たものの絶対的な結果であるから、人間が下すすべての決断や、その人間が入るすべての状況は、時間の初めから決まっていると主張したのです。そうなると、人間は何をするにしても選択の余地がない。

意志の自由を信じる人々は、量子力学の法則は何が起こるかを予測するのではなく、何がより多く、何がより少ないかだけを予測すると主張しています。したがって、すべての行動は一連のランダムな「コイントス」の結果であり、必要な前提条件のセットに遡って決定することはできません。

量子跳躍」や「量子ジャンプ」という表現は、今では普通に使われるようになりました。通常は、短期間に起こる大きな変化を意味していますが、実際には、外から入ってきた光子を吸収したときや、原子の中で電子がどのように振る舞うかを表します。実際には、電子が外部から入ってきた光子を吸収して原子核の周りのある軌道から高い軌道にジャンプしたり、光子を放出して高い軌道から低い軌道に落下したりするときの原子内での振る舞いを表す言葉です。ニールズ・ボーアらの考えは、電子は軌道間を移動するのではなく、ある軌道から消えて別の軌道に瞬間的に現れるというものでした。つまり、量子ジャンプは地球を揺るがすような変化ではなく、ある領域から別の領域への突然の小さな変化なのです。

人間が素粒子スケールのプロセスを測定して不確実性の原理が現れたとき、人間の行動は測定されているものに影響を与えたと言えます。粒子の位置を明確に示すことを目的とした測定を行うことは、必然的にその運動量に影響を与え、その位置を測定した後、できるだけ早くその運動量を測定するために何をしようと、どのような運動量が発見されるかの確率を変更しなかったことにはならない。したがって、不確実性の原理は、実験や観測の結果に影響を与える調査者によって生じるある種の干渉を説明することができます。しかし、すべてのオブザーバー効果が量子効果や不確かさの原理によるものではありません。残りは「オブザーバー効果」ですが、量子の不確実性効果ではありません。

オブザーバー効果には、私たちの通常の人間の出来事のスケールで動作するあらゆる種類のものが含まれています。人類学者が原始社会の生活について明確なアイデアを得ようとしているにもかかわらず、自分の存在が訪問先のコミュニティを動揺させた場合、その観察は非常に誤解を招くかもしれません。しかし、量子力学や不確定性原理で説明されているレベルでは、関連する相互作用はどれも起こりません。

"quantum"という言葉は、何か新しいものや強力なものを示すために広告目的で使われることがあります。例えば、小型ガソリンモーターのメーカーであるブリッグス・アンド・ストラットンには、ガソリン芝刈り機や同様の園芸用具用の4気筒低馬力モーターのラインがあり、それは"量子"と呼ばれています。

続きを読む

• 量子論入門」115頁、158頁

J.P.マケボイとオスカー・ザラテ