分子軌道とは：図解でわかる定義と電子の振る舞い（量子化学入門）

図解で学ぶ分子軌道入門：量子化学の基礎から電子の振る舞い、軌道図の読み方までわかりやすく解説。

著者: Leandro Alegsa

07-12-2025 17:09

化学では、分子軌道（MO）とは、分子内で原子が結合したときに電子に何が起こるかを説明するものです。MOは、分子内の電子の波動的な振る舞いを説明する数学的な関数です。化学者は、化学的・物理的性質を予測したり説明したりするために、このような関数を使用します。例えば、この関数は、ある特定の領域に電子が見つかる確率を教えてくれます。

化学者は通常、原子軌道を組み合わせて分子軌道の数学モデルを構築します。また、分子の各原子からのハイブリッド軌道や、原子のグループからの他の分子軌道を使うこともできます。コンピュータはこれらの機能を扱うことができる。分子軌道は、化学者が量子力学を応用して分子を研究することを可能にします。分子軌道は、分子の原子がどのようにくっついているかについての質問に答えます。軌道図の様々な丸みを帯びた形は、原子のどこに電子があるかを示しています。

基本概念：分子軌道とは何か

分子軌道（MO）は、分子全体に広がる電子の存在確率を表す波動関数の一部で、通常は「一電子軌道」として扱います。これは、個々の電子がどのようなエネルギーを持ち、どの領域にいる可能性が高いかを示します。分子軌道は原子軌道の線形結合（LCAO: Linear Combination of Atomic Orbitals）として近似されることが多く、原子軌道同士の干渉（位相が合えば構成的、逆なら破壊的）によって形とエネルギーが決まります。

結合軌道と反結合軌道

結合（ボンディング）軌道：原子軌道の位相が同じ向きで重なり、電子密度が原子間に増加します。エネルギーは元の原子軌道より低く、分子を安定化します。
反結合（アンチボンディング）軌道：原子軌道の位相が逆で重なり、原子間にノード（波動関数がゼロの面）が現れます。エネルギーは高く、電子が入ると結合を弱めます。
非結合軌道：特定の原子に局在し、他の原子との重なりが小さい軌道。エネルギーは原子軌道に近い。

電子配置とエネルギー順序：HOMOとLUMO

分子では原子と同様に、軌道に電子が入る順序があります。主に以下の規則に従います：パウリの排他原理（同一軌道におけるスピンの制限）、ハウスの法則（低エネルギー軌道から順に占有）。

HOMO（Highest Occupied Molecular Orbital）は最もエネルギーの高い占有軌道、LUMO（Lowest Unoccupied Molecular Orbital）は最もエネルギーの低い空軌道です。HOMO–LUMOギャップは、化学反応性や光学特性を決める重要な指標です（ギャップが小さいほど反応性が高く、光吸収が長波長側にずれることが多い）。

代表的な例

H2（水素分子）：2つの1s原子軌道が同位相で重なってσ（結合）軌道を作り、低エネルギーになる。逆位相で重なるとσ*（反結合）軌道ができる。
O2（酸素分子）：π*（反結合）軌道に2つの未対電子があり、そのため酸素分子は常磁性を示す（パラ磁性）。これは分子軌道理論が古典的な結合モデルより優れている例です。
CO（一酸化炭素）：HOMOは炭素側に偏った孤立電子対的性質をもち、LUMOは反結合性質を示すため、金属錯体との配位化学で特有の挙動を示します。

分子軌道図の読み方（簡単な手順）

各原子の主要な原子軌道（s, p, d など）を並べる。
エネルギーと対称性が近い軌道同士を組み合わせる（同じ対称性でしか混ざらない）。
干渉の種類（同位相＝結合、逆位相＝反結合）を決め、軌道エネルギーを並べる。
電子数に基づいて軌道に電子を入れ、HOMOとLUMOを確認する。

計算化学での扱い

実際の分子軌道は解析的に求めることが難しいため、コンピュータで近似解を求めます。代表的手法には

ハートリー–フォック（HF）法：平均場近似で一電子軌道を求める。
密度汎関数理論（DFT）：電子密度を主役にした実用的で広く使われる方法。多くの化学・材料研究で標準的。
基底関数（Basis set）：原子軌道の組み合わせに用いる関数群。大きいほど精度は上がるが計算負荷も増える。

これらの計算により、軌道の形状（電子密度分布）、エネルギー、分子の安定性、電子遷移エネルギー（光吸収スペクトル）などが得られます。

応用例：反応性、光学、磁性

分子軌道を使えば、どの部分が求核剤（電子供与体）や求電子剤（電子受容体）として働くかを予測できる（HOMOは電子供与性、LUMOは電子受容性の指標）。
光吸収は電子がHOMOからLUMOへ遷移することで説明でき、吸収波長はHOMO–LUMOギャップに対応する。
磁性は未対電子の存在（例えばO2のπ*）で説明され、磁気的性質の予測にMO理論が使われる。

まとめ

分子軌道は、分子中の電子の波動的性質を表す基本概念であり、結合の有無や強さ、反応性、光学・磁気特性を理解・予測する強力な道具です。LCAOの考え方とエネルギー準位の整理（HOMO/LUMO）を押さえることで、分子の性質を直感的かつ定量的に扱えるようになります。詳しい解析はハートリー–フォックやDFTなどの計算手法を用いて行われます。

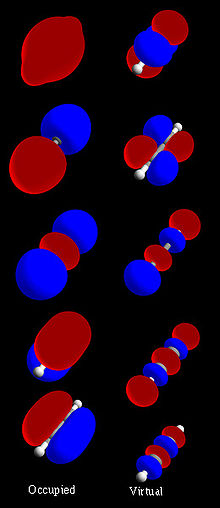
図1：完全アセチレン（H-C≡C-H）分子軌道集合

歴史

軌道という言葉は、ロバート・S・マリケンによって初めて英語で使われました。ドイツの物理学者アーウィン・シュレーディンガーは、それ以前にMOについて書いています。シュレーディンガーはそれらをEigenfunktionと呼んでいました。

物理学者マックス・ボルンは1926年に分子軌道の背後にある理論を記述しました。今日ではボルンの法則として知られ、量子力学のコペンハーゲン解釈の一部となっています。この理論は当初提案されたとき、ニールス・ボーアの原子モデルとは一致しませんでした。ボーアのモデルでは、電子は原子核の周りを「周回している」と表現されており、電子は円を描くように移動していました。しかし、Bornモデルは分子内の電子の位置を記述でき、これまで説明のつかなかった化学反応の多くを説明できることから、最終的には支持を集めるようになりました。

概要

原子軌道は、原子の中の電子の位置を予測します。分子軌道は、原子の軌道が一緒になってできたものです。分子軌道は、分子の電子配置に関する情報を与えることができる。電子配置とは、最も可能性の高い位置と、1つ（または1対）の電子のエネルギーのことです。ほとんどの場合、MOは原子軌道の直線的な組み合わせで表されます（LCAO-MO法）、特に近似的に使用されます。これは、化学者が分子内の任意の点に電子が存在する確率は、個々の原子軌道に基づいてそこに電子が存在する確率の合計であると仮定していることを意味します。LCAO-MOは分子内の結合の単純なモデルであり、分子軌道理論を研究する上で重要である。

理論化学者はコンピュータを使って、さまざまな分子（実在する分子と虚在する分子の両方）のMOを計算します。コンピュータは「雲」のグラフを描いて、電子がどの領域にどのくらいの確率で存在するかを示します。コンピュータはまた、分子の物理的性質についての情報を与えることもできます。また、分子を形成するのにどのくらいのエネルギーが必要なのかを知ることもできます。これは、化学者が小さな分子を組み合わせてより大きな分子を作ることができるかどうかを判断するのに役立ちます。

今日の計算化学のほとんどの方法は、系のMOを計算することから始まります。各MOの電場は、すべての原子の原子核と他の電子の平均的な分布によって生成されます。

アナロジー

MOを理解することは、（店の中を見ずに）大きなホームセンターの中で各従業員がどこにいるかを知る作業のようなものです。分析者は、その店で働いている従業員の数と各従業員の部署を知っています。また、従業員がお互いのつま先を踏まないことや、従業員が商品棚ではなく通路に立っていることも知っています。従業員は、顧客が他の部門の商品を探すのを手伝ったり、在庫を確認したりするために自分の部門を離れます。内部を見ないで選択された瞬間に店のすべての従業員の位置を与える分析者は、分子のMOを計算する化学者のようなものです。MOが各電子の正確な位置を伝えることができないのと同じように、各従業員の正確な位置は知られていません。結節面を持つMOは、従業員が通路を歩いているのであって、棚を通っているのではないという結論に似ています。電子は特定の原子から供給されますが、電子はその供給元の原子に関係なくMOを満たします。これは、従業員が日中、自分の部署を離れて店の他の場所を歩くようなものです。つまり、見えない店についての分析者の計算が従業員の位置についての不完全な推測であるのと同じように、MOは電子についての不完全な記述であるということです。

MOを計算するのは、ホームセンターの従業員一人一人の位置を予測するようなものです。

分子軌道の形成

理論化学者はMOを計算するためのルールを発明しました。これらのルールは、量子力学の理解に基づいています。量子力学は、化学者が電子について物理学で言われていることを利用して、電子が分子の中でどのように振る舞うかを計算するのに役立ちます。分子軌道は、原子軌道間の「許された」相互作用から形成されます。(原子軌道の対称性(群論から決定された)が互いに両立していれば、相互作用は「許される」のです)。化学者は原子軌道間の相互作用を研究しています。これらの相互作用は、2つの原子軌道間のオーバーラップ(2つの軌道がどれだけ建設的に相互作用しているかを示す指標)に由来しています。オーバーラップは、原子軌道のエネルギーが近い場合に重要です。最後に、分子内のMOの数は、分子を形成するために一緒になっている原子の原子軌道の数と等しくなければなりません。

定性的アプローチ

化学者が分子構造を議論するためには、MOの幾何学的性質を理解する必要があります。LCMO (Linear combination of atomic orbitals molecular orbitals) 法は、大まかではありますが、分子軌道の説明をしてくれます。この方法では、分子軌道は分子内の各原子のすべての原子軌道の線形結合で表されます。

原子軌道の線形結合(LCAO)

分子軌道は、1927年と1928年にフリードリヒ・フンドとロバート・S・マリケンによって初めて導入されました。

原子軌道の線形結合または分子軌道の「LCAO」近似は、1929年にジョン・レナード・ジョーンズ卿によって導入されました。彼の画期的な論文は、量子原理からフッ素分子と酸素分子の電子構造を導出する方法を示しました。この分子軌道理論への定性的なアプローチは、現代の量子化学の始まりの一部となっています。

原子軌道の線形結合（LCAO）は、分子の原子が結合したときにできる分子軌道を推測するために使うことができます。原子軌道と同様に、電子の振る舞いを記述したシュレディンガー方程式も分子軌道に対しては構築できます。原子軌道の直線的な組み合わせ（原子の波動関数の和と差）から、分子のシュレディンガー方程式の近似解が得られます。単純な二原子分子の場合、得られる波動関数は次の式で数学的に表されます。

Ψ＝_caψ_a + _cbψ_b

そして

Ψ* = _caψ_a - _cbψ_b

ここで、ΨおよびΨ*は、それぞれ、結合および反結合分子軌道の分子波動関数であり、ψ_aおよびψ_bは、それぞれ、原子aおよびbからの原子波動関数であり、_caおよび_cbは、調整可能な係数である。これらの係数は、個々の原子軌道のエネルギーと対称性に応じて、正または負にすることができる。つの原子が近くなると、その原子軌道が重なり合って電子密度の高い領域が形成されます。そのため、2つの原子の間には分子軌道が形成されます。原子は、正に帯電した原子核と負に帯電した電子が結合した分子軌道を占めることで、静電的な引力によって結合しています。

ボンディング、アンチボンディング、ノンボンディングMO

原子軌道が相互作用すると、結果として生じる分子軌道には、結合、反結合、非結合の3つのタイプがあります。

ボンディングMO。

原子軌道間の結合相互作用は、建設的な（相内の）相互作用である。
結合性MOは、それらを生成するために結合する原子軌道よりも低いエネルギーを持っています。

アンチボンディングMO。

原子軌道間の反結合相互作用は、破壊的な（相外の）相互作用である。
反結合性MOは、それらを結合して生成する原子軌道よりも高いエネルギーを持っています。

ノンボンディングMO。

非結合性MOは、対称性がないために原子軌道間の相互作用がない結果である。
非結合性MOは、分子内の1つの原子の原子軌道と同じエネルギーを持つことになります。

HOMOとLUMO

それぞれの分子軌道には、それぞれのエネルギーレベルがあります。化学者は、エネルギーレベルによってMOを並べ替えます。化学者は、電子がエネルギーレベルの低いMOを最初に満たすと仮定します。例えば、ある分子が15個の軌道を埋める電子を持っている場合、エネルギーレベルが最も低い15個のMOを埋めることになります。リストの15番目のMOは「最高占有分子軌道」（HOMO）と呼ばれ、リストの16番目のMOは「最低未占有分子軌道」（LUMO）と呼ばれます。HOMOのエネルギー準位とLUMOのエネルギー準位の差は、バンドギャップと呼ばれます。バンドギャップは、分子の励起性の指標となることがあります。電子が励起されると、電子は空のMOにジャンプします。例えば、これは何かが光を出すかどうかを推測するのに役立ちます（発光）。

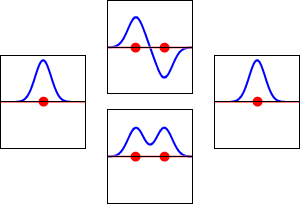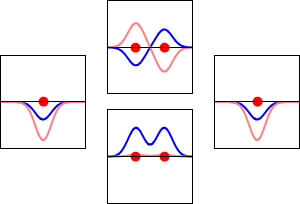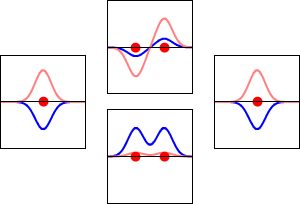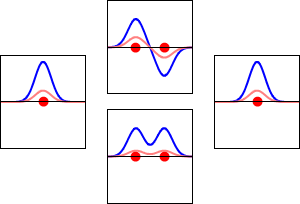
水素原子の1s軌道（左右）と、それに対応するH2分子の結合（下）と反結合（上）の電子波動関数。波動関数の実部が青の曲線、虚部が赤の曲線である。赤い点はプロトンの位置を示しています。電子の波動関数はシュレーディンガー波動方程式に基づいて振動しており、軌道はその定在波である。定在波の周波数は軌道のエネルギーに比例します。(このプロットは3次元系を1次元で切り取ったものです)。

質問と回答

Q:分子軌道とは何ですか?

A:分子軌道（またはMO）とは、分子内の電子の波動的な振る舞いを記述する数学的な関数です。原子が分子内で結合したときに電子に何が起こるかを説明し、特定の領域に電子が存在する確率を知ることができます。

Q: 化学者はどのようにして分子軌道の数学的モデルを作るのですか?

A: 化学者は通常、原子軌道を組み合わせて分子軌道の数学的モデルを構築する。分子の各原子からのハイブリッド軌道や、原子のグループからの他の分子軌道を使うこともできる。コンピュータはこれらの関数に取り組むことができます。

Q:量子力学と分子の研究にはどんな関係があるのですか?

A:分子軌道を用いると、化学者は量子力学を応用して分子を研究することができる。分子軌道は、分子内の原子がどのように結合しているかという疑問に答え、化学的・物理的特性に関する知見を与えてくれます。

Q:軌道図とは何ですか?

A: 軌道図は、原子の様々な丸みを帯びた形状に基づいて、電子が最も多く存在すると思われる場所を示す視覚的な表現である。

Q:ハイブリッド軌道はどのように機能するのですか?

A: ハイブリッド軌道は、異なるタイプの原子軌道を組み合わせて、構成要素と比較してユニークな特性を持つ新しいタイプの原子軌道にしたものです。このハイブリッド軌道は、分子軌道の数学的モデルを構築する際によく使われます。

Q:コンピュータは、分子軌道の研究にどのように役立つのでしょうか?

A:コンピュータは、分子軌道の機能を研究し、分子内の化学的・物理的特性をより正確に予測・説明することで、分子軌道の研究に役立ちます。

百科事典を検索する