ドット積

数学において、内積は2つのベクトルを入力とし、スカラー数を出力とする演算である。返される数値は、2つのベクトルの長さと、ベクトルの間の角度に依存する。スカラー積という名称は、演算結果がベクトルではなくスカラーであることを強調するために用いられる。

内積は（3次元空間において）ベクトルを結果とする外積と対照的である。

定義

2つのベクトル a = [a₁ , a₂ , ..., a_n ] と b = [b₁ , b₂ , ..., b_n ] の内積は、次のように定義されます。

a・b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {displaystyle \mathbf {a} \cdot {b} =sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+thecdots +a_{n}b_{n}}} </tr> </table $\mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

ここで、Σは総和表記（すべての項の和）、nはベクトル空間の次元を表す。

2次元では、ベクトル [a,b] と [c,d] の内積は、ac + bd です。同様に、3次元では、ベクトル [a,b,c] と [d,e,f] の内積は、ad + be + cf です。例えば、2つの3次元ベクトル [1, 3, -5] と [4, -2, -1] の内積は、次のようになります。

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) )+ ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {displaystyle [1,3,-5]\cdot [4,-2,-1]=(1tes 4)+(3tes (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.} }. $[1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.$

幾何学的解釈

ユークリッド幾何学では、内積、長さ、角度が関連している。ベクトル a に対して、内積 a - a は a の長さの二乗、つまり

a ‖ a = ‖ a ‖ 2 {displaystyle { {mathbf {a} \cdot {mathbf {a}}}=left ${\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}$

ここで、｜｜a｜｜はaの長さ（大きさ）を表し、より一般的には、bを他のベクトル

a ⋅ b = ‖ a ‖ b ‖ cos θ {displaystyle \mathbf {a} \cdot \mathbf {b} =left|mathbf {a} \right|Threshold,\left|B} {b}\Ίταμμα για για για｝ $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|\cos \theta \,$

ここで、｜｜a｜｜と｜｜b｜｜はaとbの長さを表し、θはそれらの間の角度を表しています。

この式を並べ替えると、0でない2つのベクトルがなす角の大きさを求めることができる。

θ = arccos ( a ⋅ b ‖ a ‖ b ‖ ) {}displaystyle \theta =arccos \left({}frac {{mathbf {a}}cdot {mathbf {b}}}{left|{mathbf {a}}right|}left|{mathbf {b}}right|})} {}mathbf } {{mathbf}{a} {a} {a} {b}{b}}{{b}}{}を含む $\theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)$

また、最初にベクトルを大きさで割って単位ベクトルに変換することもできる。

a ^ = a ‖ a ‖ {displaystyle {} {}boldsymbol {}hat {a}}}={frac {}mathbf {a}}{left|{mathbf {a}}right|}}} ${\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}$

とすると、角度θは次式で与えられる。

θ = arccos ( a ^ ⋅ b ^ ) {displaystyle \theta =\arccos({}boldsymbol {}hat {a}}}cdot {}boldsymbol {}hat {}})} }. $\theta =\arccos({\boldsymbol {\hat {a}}}\cdot {\boldsymbol {\hat {b}}})$

90°の余弦が0であるように、直交（垂直）する2つのベクトルの内積は常に0である。さらに、2つのベクトルは、その内積が0であり、かつ、その長さが0でない場合にのみ、直交していると考えることができる。この性質は、直交性の条件を調べるための簡単な方法を提供します。

これらの性質は、特に2次元や3次元での内積の定義にも使われることがあり、この定義は上記の定義と同等である。高次元では、この式を使って角度の概念を定義することができる。

幾何学的特性は、基底が正規直交であること、すなわち単位長さを持つ一対の垂直なベクトルから構成されていることに依存します。

スカラー投影

aとbがともに長さ1の場合（つまり単位ベクトル）、その内積は両者のなす角の余弦を与えるだけである。

bだけが単位ベクトルなら、a-bの内積は｜a｜cos(θ)、すなわちaのb方向への射影の大きさを与え、方向が逆ならマイナス記号を付ける。これを a の b へのスカラー投影、または b の方向への a のスカラー成分と呼ぶ（図参照）。ドットプロダクトのこの性質は、いくつかの有用な応用がある（たとえば、次節参照）。

aもbも単位ベクトルでない場合、例えばaのb方向への射影の大きさは、b方向の単位ベクトルがb / |b|なので、a - (b / |b|)となります。

ローテーション

ベクトルaを表現する直交基底の回転は、aに回転行列Rを掛けることで得られます。

例えば、次のようにします。

B₁ = {x, y, z} と B₂ = {u, v, w} は同じ空間 R³ の異なる二つの直交正規基底で、B₂ は B₁ をただ回転させることで得られます。
a₁ = (a_x , a_y , a_z ) は，B₁ の観点からベクトル a を表す。
a₂ = (a_u , a_v , a_w ) は，回転した基底B₂ の観点から同じベクトルを表します．
u₁ , v₁ , w₁ は，B₁ の項で表される回転した基底ベクトル u, v, w である．

そして、B₁ から B₂ への回転は、以下のように行われる。

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ・ a 1 v 1 ・ a 1 w 1 ・ a 1 ] = [ a u a v a w ] .{\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf{v}_{1}cdot {a}_{1}} {w}_{1}cdot {a}_{1}} end{bmatrix}}={begin{bmatrix}a_{u}} {v}} {w} {a}_{w} {bmatrix}}となる。} ${\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}.$

回転行列Rは、回転した基底ベクトルu₁ , v₁ , w₁ を行として組み立てられており、これらのベクトルは単位ベクトルであることに注意されたい。定義によれば、Ra₁ は、R の3行のそれぞれとベクトル a₁ との間の一連のドット積からなる。これらのドット積のそれぞれは、回転した基底ベクトルの方向における a のスカラー成分を決定する（前節を参照）。

₁ が列ベクトルではなく行ベクトルである場合、R はその列に回転した基底ベクトルを含まなければならず、₁ を後乗せしなければならない。

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ・ a 1 v 1 ・ a 1 w 1 ・ a 1 ] = [ a u a v a w ] .表示スタイル {{mathbf {a}_{2}={mathbf {a}}_{1}{mathbf {R}}={}begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}} end{bmatrix}}={{begin{bmatrix}{{mathbf {u}}_{1}} {cdot {}mathbf {a}}_{1}&{mathbf {v}}_{1}} {cdot {}mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.} ${\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}.$

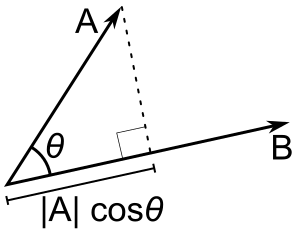
A - B = |A| |B| cos(θ)。| A| cos(θ)はAのBへのスカラー投影である。

物理学

物理学では、マグニチュードは物理的な意味でのスカラー、すなわち座標系に依存しない物理量で、単なる数値ではなく、数値と物理単位の積として表される。内積もこの意味でスカラーであり、式で与えられる、座標系に依存しない物理量である。例

機械的な仕事とは、力と変位ベクトルの内積である。
磁束は、磁場と面積ベクトルの内積である。
体積流量は、流体速度と面積ベクトルの内積である。

プロパティ

a, b, cを実数ベクトル、rをスカラーとすると、以下の性質が成り立つ。

ドットプロダクトは可換である。

a a ⋅ b = b ⋅ a . { \displaystyle \mathbf {a} \cdot \mathbf {b} = \mathbf {b} .\cdot \mathbf {a} .} $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} .$

内積はベクトル加算に対して分配的である。

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c .{ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ+mathbf {a} \cdot \mathbf {c} .} $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

ドットプロダクトはバイリニアです。

a・( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) .{ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ} $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

スカラー値との乗算では、ドットプロダクトが満たされる。

( c 1 a ) ・ ( c 2 b ) = ( c 1 c 2 ) ( a ・ b ) {displaystyle (c_{1}mathbf {a} )\cdot (c_{2}mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} ) } }. $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )$

(この最後の2つの性質は、最初の2つの性質から導かれます）。

2つの非ゼロベクトルa、bが垂直であるのは、a - b = 0のときだけである。

普通の数の掛け算では、ab＝acとすると、aが0でない限りbは必ずcと等しくなるが、内積は打ち消し法則に従わない。

a - b = a - c で a ≠ 0 ならば、分配法則により a - (b - c) = 0 と書ける。上の結果から、これは a が (b - c) に垂直であることを意味しているだけなので、やはり (b - c) ≠ 0 となり、b ≠ c となる。

基底が正規直交であれば、ドットプロダクトは基底の等尺性変化（原点を固定したまま回転、反射、組み合わせ）に対して不変である。上述の幾何学的解釈は、この性質に依存している。つまり、任意の次元数の正則空間において、直交行列に基づく座標変換のもとでは、点積は不変である。これは、次の2つの条件に対応する。

新しい基底は再び正則化される（すなわち、古い基底で表現された正則化される）。
新しい基底ベクトルは古いものと同じ長さ（つまり、古い基底から見て単位長）である。

aとbを関数とすると、a - bの微分はa' - b + a - b'である。

三重積展開

これは、内積と外積を含む非常に便利な恒等式（ラグランジュの公式とも呼ばれる）です。次のように書きます。

a × ( b × c ) = b ( a・c ) - c ( a・b ) {displaystyle \mathbf {a} \times (\mathbf {b} \times {c} )=⃛mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-⃛displaystyle\γmathbf {c} (\mathbf {a} γcdot γmathbf {b} )} ←クリック $\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )$

という式がありますが、どのベクトルがドットで結ばれているかを意識して、「BACマイナスCAB」と覚えるとわかりやすいでしょう。この式は、物理学でベクトルの計算を簡単にするためによく使われる。

幾何学的解釈の証明

Rの要素ⁿ を考える。

v = v 1 e ^ 1 + v 2 e ^ 2 + ... ....................。+ v n e ^ n .Filter=v_{1} {hat {e}} =v_{1}{hat {e}}1}+v_{2} {hat {e}} のようになります。_{2}+...+v_{n} {hat {e}} のようになります。_{n}.\,} $\mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,$

ピタゴラスの定理を繰り返し適用すると、その長さ｜v｜が得られる。

| v｜2＝v1 2＋v2 2＋ ... ...+ v n 2 .{|displaystyle |mathbf {v}|^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,} $|\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,$

しかし、これは

v ⋅ v = v 1 2 + v 2 2 + ....+ v n 2 , { {displaystyle \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,} }. $\mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,$

ということで、ベクトルvとそれ自身の内積をとると、ベクトルの長さの2乗が得られると結論づけられます。

レンマ1

v ⋅ v = | v | 2 .|^{2}.\,} $\mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,$

ここで、原点から角度θだけ離れて伸びている2つのベクトルa、bを考える。第3のベクトルcは次のように定義することができる。

c = d e f a - b .{Ίταμμα\ Ίταμμα για για για για}{=}} \mathbf {a} -mathbf {b} .\,}. $\mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,$

は、辺がa,b,cの三角形を作る。余弦の法則によれば

| c｜2 =｜a｜2 +｜b｜2 - 2｜a｜b｜cos θ .|^{2}=|mathbf {a}.|^{2}=|mathbf {a}|^{2}+|mathbf {b}|^{2}-2 ||mathbf {a}|||mathbf {b}|cos \theta .\, }. $|\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

レンマ1により、2乗の長さにドット積を代入すると、次のようになる。

c・c = a・a + b・b - 2 | a | | b | cos θ .{ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ。\cdot \mathbf {c} =mathbf {a} \cdot +mathbf {b} {cdot =mathbf {a} +mathbf {b\cdot \mathbf {b} -2|mathbf {a}|||mathbf {b}|cos ㊞㊞ $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$ (1)

しかし、c≡a - bなので、次のようにもなります。

c ⋅ c = ( a - b ) ⋅ ( a - b ) {displaystyle \mathbf {c}.\cdot \mathbf {c} =(\mathbf {a} - Neither {b} )\cdot (\mathbf {a} - Neither {b} )\,} $\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,$ ,

に拡大し、分配法則により

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) .{ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ。\cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} $\mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,$ (2)参照。

2つのc - c式、(1)と(2)を統合すると、次のようになります。

a・a + b・b - 2 ( a・b ) = a・a + b・b - 2 | a | | b | cos θ .{ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ\mathbf {b} -2(\mathbf {a} \mathbf {b} )= \mathbf {a} \mathbf {a} + Neither Neither!\cdot \mathbf {b} -2|mathbf {a}|||mathbf {b}||cos｝ $\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

両辺から a - a + b - b を引き、-2 で割ると残ります。

a・b = | a | | b | cos θ .{|||mathbf {a} =|mathbf {a}|||mathbf {b}|cos ㊞㊞ θ｝ $\mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,$

Q.E.D.

一般化

内積はドットプロダクトを抽象的なベクトル空間に一般化したもので、通常⟨ a , b ⟩ {displaystyle \langle {a}, \mathbf {b} で示されます。\rangle }. $\langle \mathbf {a} \,,\mathbf {b} \rangle$ .ドットプロダクトの幾何学的解釈により、このような内積空間におけるベクトルaのノルム｜｜a｜｜は次のように定義されます。

‖ a ‖ = ⟨ a , a ⟩ {displaystyle \|pathbf {a} \|={sqrt {langle \,,\mathbf {a} \rangle }}} $\|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}$

によって、長さを一般化し、2 つのベクトル a と b の間の角度 θ を一般化するようなものである。

cos θ = ⟨ a , b ⟩ ‖ a‖ ‖ b ‖ .\Ίταν για για για για για για για για για για\|}}.} $\cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}.$

特に、2つのベクトルは、その内積が0であれば、直交しているとみなされる

⟨ a , b ⟩ = 0. {displaystyle \langle {a}, \mathbf {b} {displaystyle} {a}, \mathbf {b}.\rangle =0.}. $\langle \mathbf {a} \,,\mathbf {b} \rangle =0.$

複素数のエントリーを持つベクトルでは、与えられた内積の定義を用いると、全く異なる幾何学的性質になります。例えば、ベクトルとそれ自身の内積は任意の複素数になり、ベクトルがゼロベクトルでなくてもゼロになることがあります。これは、長さや角度などの概念に重大な影響を与えます。スカラー積の対称性とバイリニアの性質を放棄する代わりに、多くの幾何学的性質を救うことができる。

a ⋅ b = ∑ a i b i ¯ {displaystyle \mathbf {a} \cdot \mathbf {b} =sum {a_{i}{overline {b_{i}}}}}}}。 $\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}$

ここで、b_i は b_i の複素共役です。このとき、任意のベクトルとそれ自身のスカラー積は非負の実数であり、ゼロベクトルを除いて非ゼロです。しかし、このスカラー積は b に対して線形ではなく（むしろ共役線形）、スカラー積は対称でもない、なぜなら

a ⋅ b = b ⋅ a ¯ {displaystyle \mathbf {a} \cdot \mathbf {b} ={overline {} {} {b}\cdot \mathbf {a} }} .}}} $\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}$ .

この種のスカラー積は非常に有用であり、エルミート形式や一般的な内積空間の概念につながる。

フロベニウス内積は、ドットプロダクトを行列に一般化したものです。同じ大きさの2つの行列の対応する成分の積の和として定義される。

テンソルへの一般化

次数nのテンソルと次数mのテンソルの内積は、次数n+m-2のテンソルとなる。内積は両テンソルの1つのインデックスに渡って乗算と和算をすることで得られる。A {displaystyle \mathbf {A}} とB {displaystyle｜displaystyle｜displaystyle} $\mathbf {A}$ とB {displaystyle \mathbf {B} } が2つのテンソルである場合、内積を求める。} $\mathbf {B}$ が要素表現A i j ... k ℓ ... {\displaystyle A_{ijdots }^{kell }} $A_{ij\dots }^{k\ell \dots }$ とB m n ... p ... i {\displaystyle B_{mndots }^{p{dots }i} $B_{mn\dots }^{p{\dots }i}$ であるならば、点積A・B {displaystyle \mathbf {A}の要素である。｝\cdot \mathbf {B} } は次のように与えられます。} は次式で与えられる。 $\mathbf {A} \cdot \mathbf {B}$

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ...p ...i {displaystyle A_{ij }^{kell \dots }B_{mndots }^{p{dots }i}=SUM _{i=1}^{n} A_{ij }^{kell｜dots }B_{mndots }^{p{dots }i}} {displaystyle A_{ij }^{kell｜dots }^{p{dots }} =SUM $A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}$

この定義は、ベクトルに適用する場合は標準的なベクトルの内積に、行列に適用する場合は行列の乗算に自然に還元される。

2つのインデックスの掛け算や足し算を表現するために2重内積が使われることがある。2つの2次テンソル間の2重内積はスカラーである。

質問と回答

Q: 数学の内積とは何ですか?

A: 内積は2つのベクトルを入力とし、スカラー数を出力とする演算である。

Q: ドット積は何に依存しますか?

A: 内積は両ベクトルの長さと両ベクトル間の角度に依存します。

Q: ドット積の名前が中央のドット"-"に由来するのはなぜですか?

A: この演算を表すのによく使われる中心点"-"に由来しています。

Q: ドット積の別名は何ですか?

A: 別名はスカラー積で、結果の（ベクトルではなく）スカラー性を強調しています。

Q: 3次元空間における内積と外積の違いは何ですか?

A: 点積は結果としてスカラー数を生成しますが、クロス積は結果としてベクトルを生成します。

Q: ドット積は数学で何に使われますか?

A: 内積は2つのベクトルが垂直（90度の角度を持つ）かどうかを判断したり、あるベクトルを別のベクトルに投影したりするのに使われます。

Q: 高次元空間でも使えますか?

A: はい、定義を一般化することで高次元空間に拡張できます。