調和級数

数学では、ハーモニック級数は発散無限級数である。

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯⋯ {\displaystyle } {sum _{n=1}^{\infty } {\frac {1}{n}=1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{3}+{\frac {1}{4}+{\frac {1}{5}+cdots}} } {\frac {1}{5}+cdots}} {\frac {1}{5}+cdots}} } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

発散とは、項を増やしても和が大きくなるのを止めないことを意味します。それは一つの有限値に向かっていくわけではありません。

無限とは、いつでも別の項を追加できることを意味します。直列に最終項はありません。

名前の由来は、音楽における倍音の考え方から来ている：振動する弦の倍音の波長は、弦の基本波長の1/2、1/3、1/4などである。最初の項を除いて、系列のすべての項は、その両側の項の調和的平均です。調和平均という言葉も音楽から来ています。

歴史

調和級数が発散するという事実は、14世紀にニコル・オレスメによって初めて証明されたが、忘れ去られていた。17世紀にはピエトロ・メンゴリ、ヨハン・ベルヌーイ、ヤコブ・ベルヌーイによって証明がなされた。

ハーモニック・シーケンスは建築家によって使用されてきた。バロック時代の建築家は、間取り図、立面図、教会や宮殿の建築細部間の関係でそれらを使用していました。

発散

調和級数の発散の証明はいくつか知られています。そのうちのいくつかを以下に示す。

比較試験

発散を証明する1つの方法は、各分母を2つの次の最大乗に置き換えた別の発散級数と調和級数を比較することです。

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {displaystyle {begegin{aligned}&&&♪1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}+{\frac {1}{7}}++{\frac {1}{8}+{\frac {1}{8}+{\frac {1}{9}+\cdots}1+{\frac {1}{2}}}+{\frac {1}{1}{2}}+{\frac {1}{1}{2}}}+{\mathbf {4}♪}}+{\frac {1}{4}}+{\frac {1}{color {red}}}}+{\mathbf {8}。♪}}}+{\frac {1}{color {red}}{\mathbf {8}}♪}}}+{\frac {1}{color {red}}{\mathbf {8}}♪}}+{\frac {1}{8}}+{\frac {1}{color {red}}}+{Mathbf {16}}。♪}}}+\cdots ¶+\end{aligned}}}}}。 ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

調和級数の各項は第2級数の対応する項以上であり、したがって調和級数の和は第2級数の和以上でなければならない。ただし、第２系列の和は無限大である。

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {displaystyle {begegin{aligned}&{}1+\left({\frac {1}{2}}right)++left({\frac {1}{4}}!+!+\!♪♪ +\cdots ≪12pt≫={}&1+{\frac {1}{2}+{\frac {1}{2}+{\frac {1}{2}+{\frac {1}{2}+{\frac {1}{2}++cdots =infty \end{aligned}}}}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

それは（比較検定によって）調和級数の和も同様に無限大でなければならないことを次のように示しています。より正確には、上の比較によって、次のことが証明されます。

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle ｻﾞﾑ _{n=1}^{2^{k}} {\frac {1}{n}}geq 1+{\frac {k}{2}}}}}}}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

すべての正の整数 $k$ に対して

この証明は、1350年頃にニコル・オレスメによって提案されたもので、中世数学の頂点とされています。これは今日でも数学の授業で教えられている標準的な証明です。

インテグラルテスト

調和級数が発散することは、その和を不適切な積分と比較することで証明できます。右図のような長方形の配置を考えてみましょう。各長方形の幅は1単位，高さは1/n単位であるから，無限にある長方形の面積の合計が調和級数の和となる。

矩形の面積 = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯⋯ {\\ style {begin{array}{c}{text{area of}}}\\\{text{rectangles}}end{array}}=1+{frac {1}{2}+{frac {1}{3}+{frac {1}{3}+{frac {1}{4}+{\frac {1}{5}+{cdots}}}\ ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

1から無限大までの曲線 $y = 1$ /xの下の総面積は発散性のある不適当な積分で与えられます。

曲線の下の面積 = ∫ 1 ∞ 1 x d x = ∞ .♪\\ style {begin{array}{c}{area under}}}}=int _{1}^{\infty}},dx=\infty .} ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

この面積は完全に長方形の中に含まれているので、長方形の総面積も無限大でなければならない。これは次のことを証明しています。

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) .♪\displaystyle sum _{n=1}^{k}^{k}{\frac {1}{n}}>int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).} $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

この引数の一般化は積分テストとして知られています。

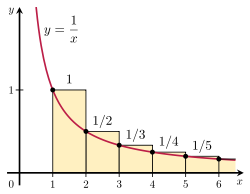
積分試験の図解。

発散率

調和級数は非常にゆっくり発散します。例えば、最初の¹⁰⁴³項の和は100以下です。これは、系列の部分和が対数的に成長するからです。特に

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle ｻﾞﾑ _{n=1}^{k}}{ﾌﾗｯｸ {1}{n}}=\ln k+gamma +varepsilon _{k}\leq (lln k)+1}. $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

ここで $γはオイラー-$ マスチェローニ定数であり、 $ε k ~$ 1/2kは $kが$ 無限大になるにつれて0に近づく。レオンハルト・オイラーはこの両方を証明し、素数の逆数だけを含む和も発散することを証明しました。

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ .} $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

部分的な合計

最初の30の調和数
$n$	高調波級数の部分和、 $Hn$
$n$	分数表示		十進数	相対的な大きさ
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

発散調和級数の有限部分和。

H n = ∑ k = 1 n 1 k , {displaystyle H_{n}=\ sum _{k=1}^{n}{frac {1}{k}},}. $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

を調和数と呼びます。

$Hn$ と $ln nの$ 差はオイラー-マスチェローニ定数に収束する。任意の2つの調和数の間の差は決して整数ではない。 $H 1 = 1を除いて、調和数が整数$ になることはありません。

関連シリーズ

交流高調波系列

シリーズ

は交互調和級数として知られています。この級数は交互級数検定で収束します。特に、和は2の自然対数に等しい。

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2.{displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{4}}+{\frac {1}{5}}-cdots = ln 2. $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

交互高調波級数は、条件付きで収束しますが、絶対的に収束するわけではありません。級数の項を系統的に並べ替えると、一般的に和は異なり、並べ替えに依存して無限大になることもあります。

交番調和級数の公式は、メルカトル級数、自然対数のテイラー級数の特殊なケースです。

関節のテイラー級数から関連する級数を導出することができます。

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯⋯ 4 .{displaystyle sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+cdots ={\frac {1}{7}}+{4}}.} $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

これはライプニッツシリーズとして知られています。

一般的な高調波級数

一般的な高調波級数は

∑ n = 0 ∞ 1 a n + b , {displaystyle \ sum _{n=0}^{\infty} }{\frac {1}{an+b}}, }。 $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

ここで、 $ａ\neq ０$ 、 $ｂは$ 実数であり、ｂ／ａは０または負の整数ではない。

高調波級数との限界比較試験により、一般的な高調波級数もすべて発散します。

$ピーけい$ れつ

調和級数の一般化は、次のように定義される $p$ 級数（または超調和級数）です。

∑ n = 1 ∞ 1 n p {\displaystyle ｻﾑ _{n=1}^{\infty}}{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

$p = 1$ のとき、 $p 系列は$ 発散する高調波系列です。積分検定かコーシー凝縮検定のいずれかで、 $p 系列$ はすべての $p > 1 に$ 収束し $(この場合、これ$ をオーバーハーモニック級数と呼ぶ)、すべての p $\leq 1 に$ 発散することを示しています。 $p > 1の$ 場合、p $系列の$ 和はζ( $p)、すなわち、$ pで評価されるリーマン・ゼータ関数となります。

$p = 2の$ 和を求める問題はバーゼル問題と呼ばれ、レオンハルト・オイラーはそれが $π$ ²/6であることを示した。 $p = 3の$ 和の値はアペリ定数と呼ばれ、ロジャー・アペリがそれが不合理な数であることを証明したことから、アペリ定数と呼ばれています。

ｌｎ系列

$p-$ 系列に関連するのはln-系列で、次のように定義されています。

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle ｻﾑ _{n=2}^{in\fty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

これは、 $p \leq 1で$ 発散しますが、すべての $p > 1で$ 収束することを積分検定で示すことができます。

$φ$ 系列

以下のような凸の実数関数 $φ$ に対して

limleasesZs_2006 CATEGORIES_UP u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {displaystyle \limsup _{u\to 0^{+}}{\frac {\frac {u}{2}\right}}}{\varphi (u)}}<{\frac {1}{2},},}<{\frac {1}{2},},}。 $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

系列

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle ｻﾞﾑ _{n=1}^{\infty} }Var\phi ¶left({\frac {1}{n}right})} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

は収束している。^[]

ランダムハーモニック級数

∑ n = 1 ∞ s n n , {displaystyle \ sum _{n=1}^{\infty}}{\frac {s_{n}}{n}}, }。 $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

ここで、 $snは$ 独立しており、等しい確率1/2で値+1と-1をとる同一分布のランダム変数であり、確率論では、確率1で収束するランダム変数の系列のよく知られた例です。この収束の事実は、Kolmogorovの3系列定理または密接に関連するKolmogorovの最大不等式のいずれかの簡単な結果です。アルバータ大学のByron Schmulandは、ランダムハーモニック級数の性質をさらに調べ、収束級数がいくつかの興味深い性質を持つランダム変数であることを示しました。特に、+2または-2で評価されるこのランダム変数の確率密度関数は、0.124999999999999999999999999999999999999999999999999999764...という値をとり、1/8と10^{-42以下の差があります}。Schmulandの論文では、なぜこの確率が1/8に近いが、正確ではないのかを説明しています。この確率の正確な値は，無限余弦積積分 $C2を π$ で割ったもので与えられます．

劣化調和級数

9という数字が分母のどこかに現れる項がすべて取り除かれた枯渇調和級数は、収束し、その値が80以下であることを示すことができます。実際には、任意の桁の文字列を含む項（任意の基底）がすべて削除されると、系列は収束します。

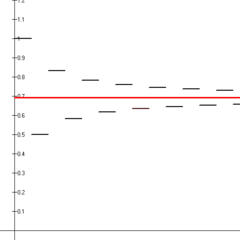
交番調和級数の最初の14個の部分和（黒線部分）は、2の自然対数（赤線）に収束することが示されている。

アプリケーション

調和級数は逆に直感的であることがあります。級数の項が小さくなり、ゼロに向かっていくにもかかわらず、発散級数だからです。調和級数の発散は、いくつかのパラドックスの原因となっています。

輪ゴムの上のミミズ」です。輪ゴムが一様に伸びると同時に、無限に伸びる1メートルの輪ゴムの上を虫が這っているとしましょう。虫が1分間に1cm移動し、ゴムバンドが1分間に1m伸びたとすると、虫はゴムバンドの端にたどり着くことができるでしょうか？答えは、反直感的に「はい」となります。

1 100 ∑ k = 1 n 1 k .{\displaystyle {frac {1}{100}\sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

級数は $nが$ 大きくなるにつれて任意に大きくなるので、最終的にはこの比が1を超えなければならず、これはワームが輪ゴムの端に到達したことを意味します。しかし、このときの $nの$ 値は、¹⁰⁴³分（^1037年）を超えるe $100$ 程度と非常に大きくなければなりません。調和級数は発散しますが、発散は非常にゆっくりです。

ジープの問題は、燃料を運ぶ能力が限られている車が砂漠を横断する際に、ルートに沿って燃料を落としながら横断するために必要な燃料の総量を問う問題である。与えられた量の燃料で車が移動できる距離は、対数的に成長する調和級数の部分和に関係しています。そのため、必要な燃料は目的の距離に応じて指数関数的に増加します。

ブロック積み問題: 同一のドミノの集合体が与えられた場合，テーブルの端にそれらを積み上げて，テーブルの端から落ちずに垂れ下がるようにすることができる．直感的ではない結果は，はみ出しを好きなだけ大きくする方法で積み重ねることができるということである．つまり、十分なドミノがあることを条件に。

プールの壁に触れるたびにスピードを上げていくスイマー。10mのプールを2m/sの速度で渡り始め、渡るたびに2m/sが加算されていく。理論的には、泳ぎ手の速度は無限ですが、その速度に到達するためには、プールを何回も渡る必要があり、例えば、光速（特殊相対性理論を無視して）に到達するためには、1億5000万回プールを渡る必要があります。この大きな数とは逆に、ある速度に到達するのに必要な時間は、任意の与えられた数のプールを横断したときの系列の和に依存します。

10 2 ∑ k = 1 n 1 k .{\displaystyle {10}{2}\sum _{k=1}^{n}{\frac {1}{k}}.} ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

合計を計算すると、光速に到達するまでに必要な時間はわずか97秒であることがわかります。

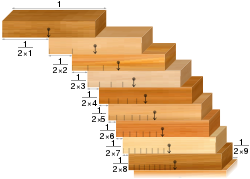
ブロック積み問題：任意の幅の高調波系列の橋の裂け目に応じて整列したブロック。

質問と回答

Q:調和級数とは何ですか?

A:調和級数とは無限発散級数で、各項は1÷その位置で等しくなります。

Q:系列が発散するとはどういう意味ですか?

A:発散とは、項を追加しても、和が大きくなることを止めず、一つの有限な値に向かわないことを意味します。

Q:級数が無限大であるとはどういう意味ですか?

A:無限とは、常に別の項を加えることができ、系列に最終項がないことを意味します。

Q:この系列の名前はどこから来たのですか?

A:この級数の名前は、音楽における倍音の考え方に由来しています。倍音の波長は、弦の基本波長の1/2、1/3、1/4などになっているのです。

Q:ハーモニックス平均とは何ですか?

A:調和平均とは、ある数列のすべての項が、隣接する項の調和平均と等しいことです。この言葉も音楽からきています。

Q:この数列の各項はどのように計算するのですか?

A:この数列の各項は、1を数列内の位置で割ることで計算できる（1/n）。

調和級数

歴史

発散