表面積分（曲面積分）とは｜定義・計算法・スカラー／ベクトル場と電磁気学への応用

数学において、曲面積分は曲面（空間的に設定された曲線でもよい）上の定積分である。線分積分が1次元、1変数を扱うように、曲面積分は2次元に沿った2重積分と考えることができる。曲面が与えられると、そのスカラー場（数値を値として返す関数）とベクトル場（ベクトルを値として返す関数）に対して積分を行うことができます。

表面積は物理学、特に古典的な電磁気学の理論で応用されている。

基本的な定義と記法

曲面 S をパラメトリック表示 r(u,v) で与えるとき、曲面上のスカラー場 f とベクトル場 F に対する曲面積分は次のように定義される。

スカラー場の曲面積分（面積に関する積分）：
∬_S f dS = ∬_D f(r(u,v)) |r_u × r_v| dudv
ここで r_u = ∂r/∂u, r_v = ∂r/∂v、|r_u × r_v| は面要素の大きさを与える。
ベクトル場の曲面積分（フラックス積分）：
∬_S F · n dS = ∬_D F(r(u,v)) · (r_u × r_v) dudv
ここで n は通常の向きに従った単位法線ベクトルで、r_u × r_v の方向が法線の向きを示す（符号に注意）。

面要素の具体例

グラフ z = g(x,y) の場合（S = {(x,y,g(x,y))}）：
dS = sqrt(1 + g_x^2 + g_y^2) dx dy
球面（半径 R） を球面座標で表すと r(θ,φ) = (R sinθ cosφ, R sinθ sinφ, R cosθ)（0 ≤ θ ≤ π, 0 ≤ φ < 2π）。
面要素は dS = R^2 sinθ dθ dφ であり、球面全体の面積は 4πR^2 となる。
円柱（半径 a, 高さ h） の側面：パラメータ (θ,z) → r(θ,z) = (a cosθ, a sinθ, z) で、dS = a dθ dz など。

計算の手順（実用的な流れ）

曲面 S を適切にパラメータ r(u,v) で表す（または z = g(x,y) の形に書く）。
必要ならば r_u と r_v を計算し、r_u × r_v の大きさを求める。
積分する関数 f(r(u,v)) または F(r(u,v))·(r_u × r_v) を書き下す。
パラメータ領域 D 上で二重積分を評価する（必要に応じて座標変換を行う）。
向き（法線ベクトルの向き）に注意して符号を確かめる。

向き・境界・定理との関係

向きの重要性：ベクトル場のフラックスを扱うとき、曲面に法線方向が定まっていないと値は定義できない。同じ曲面でも法線を反転すると積分値は符号が反転する。
ストークスの定理：曲面 S の境界 ∂S を向くとき、∬_S (curl F)·n dS = ∮_{∂S} F·dr。これは曲面積分と線積分を結ぶ重要な関係である。
発散定理（ガウスの定理）：閉曲面 ∂V に対して ∬_{∂V} F·n dS = ∭_V div F dV。閉曲面上のフラックスを体積内の発散に変換する。

電磁気学への応用例

ガウスの法則（静電場）：電場 E に対して、閉曲面 S を貫く電気力線の総数（フラックス）は包囲する電荷 Q_enc に比例する。式で表すと ∬_S E·dA = Q_enc/ε0 。これは曲面積分の直接的な応用である。
磁束とファラデーの法則：磁束 Φ_B = ∬_S B·dA を定義し、磁束の時間変化が誘導起電力（起電力 ε = - dΦ_B/dt）を生む。ここでも曲面積分が中心的役割を果たす。
境界条件やフラックスの計算：導体表面や誘電体の界面での場の正確な振る舞いを解析する際に曲面積分は頻繁に用いられる。

よくある例題（簡単な結果）

球面（半径 R）の面積：A = ∬_S dS = ∫_0^{2π} ∫_0^π R^2 sinθ dθ dφ = 4πR^2。
グラフ z = g(x,y) の面積：A = ∬_D sqrt(1 + g_x^2 + g_y^2) dx dy。

注意点・拡張

曲面が自己交差する場合やパラメータ表示が一意でない場合は注意が必要。通常は局所的にパラメトリゼーションをとって積分を定義する。
滑らかでない境界や特異点があるときは、極限や分割を用いて積分を定義することが多い。測度論的な扱い（面積測度）に拡張することも可能である。
微分形式を用いると一般次元での「面積」や「フラックス」を統一的に扱える（高度な視点）。

上記は曲面積分の定義、計算法、物理への応用を概観したものである。具体的な問題ではパラメータの取り方、積分領域の設定、法線の向きに特に注意して計算する。

表面積の定義は、表面を小さな表面要素に分割することに依存する。

1枚の表面要素の説明図。これらの要素は、リミッター処理により、表面に近似するように無限に小さくなる。

スカラー場の表面積分

スカラー場 f が定義された表面 S を考える。S をある物質でできていると考え、S の各 x に対して数 f(x) を x での物質の密度とすると、S 上の f の表面積分は S の単位厚さあたりの質量となります（これは表面が無限大に薄い殻である場合のみ当てはまります。表面積分を計算する一つの方法は、表面を非常に小さな断片に分割し、それぞれの断片の密度がほぼ一定であると仮定し、断片の密度にその面積を乗じてそれぞれの断片の単位厚さあたりの質量を求め、得られた数値を合計してSの単位厚さあたりの総質量を求めることである。

表面積分の明示的な公式を求めるために、数学者は球面上の緯度・経度のような曲線座標系をS上で考え、Sをパラメータ化します。このようなパラメタリゼーションを x(s, t) とすると、 (s, t) は平面上のある領域 T で変化します。このとき、表面積分は次式で与えられる。

∫S f d S = ∬T f ( x ( s , t ) )| ∂ x ∂ s × ∂ t | d s d t {displaystyle \int _{S}f,dS=iint _{T}f(\mathbf {x} (s,t))\left|{Partial \mathbf {x}} {Displaystyle \int_2202↩ x ∂ t} ∂ x ∂ s × ∂ t {displaystyle \int _{Sm_2202↩ s × ∂ t\Όταμμα για για για για για για για για για για\over \partial t}right|ds,dt}. $\int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt$

ここで、右辺の棒の間の式は x(s, t) の偏導関数の逆積の大きさである。

例えば、ある一般的な関数形、z = f ( x , y ) {displaystyle z=f,(x,y)} $z=f\,(x,y)$ の表面積を求めるには、次のようにします。

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ‖ d x d y {displaystyle A=int _{S},dS=iint _{T} left|{partial \mathbf {r}} {dSm_2202↩ r ∂ y ‖ d x d y\Όταμμα ταμμα ταμμα ταμμα ταμμα\Ίταν ταν για｝ $A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy$

ここで、r = ( x , y , z ) = ( x , y , f ( x , y ) )である。{displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))} $\mathbf {r} =(x,y,z)=(x,y,f(x,y))$ .ということは、∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) となります。{￤displaystyle {partial ￤mathbf {r｝∕ x = (1,0,f_{x}(x,y)) ${\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))$ とし、∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) とする。{displaystyle {partial \mathbf {r}∕ y}=(0,1,f_{y}(x,y))} ${\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))$ .というわけで。

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( − ∂ f ∂ x , − ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=iint _{T}left {left(1,0,{}partial f \over x}right)\times \left(0,1,{}partial f \over y}right)\right|dx},dy}A&{}=T}iint _{T}left {left(-{partial f \over \partial x},-{partial f \over \partial y},1right)\right|dx´,dy´&{}=Tint _{T}{}sqrt {}left({}partial f \over \partial x}right)^{2}+left({}partial f \over \partial y}right)^{2}+1}} {},\,dx,dy end{aligned}}} ${\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}\,\,dx\,dy\end{aligned}}$

これは、一般的な関数形状の表面積を表す式である。上の2行目のベクトルは、表面の法線ベクトルとして認識することができる。

クロスプロダクトが存在するため、上記の式は3次元空間に埋め込まれたサーフェスに対してのみ有効であることに注意してください。

ベクトル場の表面積分

S上のベクトル場v、すなわちS内の各xに対してv(x)がベクトルであることを考える。

表面積分は、スカラー場の表面積分の定義に従って成分的に定義することができ、その結果はベクトルである。例えば、帯電した表面によるある定点での電場や、シート状の物質によるある定点での重力がこれにあたります。また、表面を通る磁束を計算することもできる。

また、数学者はベクトル場の法線成分を積分することができ、その結果はスカラーになる。例えば、S を流れる流体の場合、v(x) は x における流体の速度である。

この図は、ベクトル場が各点でSに接する場合、流体はSと平行に流れるだけで、内側にも外側にも流れないので、フラックスはゼロであることを意味している。このことは、もしvがSに沿って流れるだけでなければ、つまりvが接線成分と法線成分の両方を持つのであれば、法線成分だけがフラックスに寄与することも意味している。このことから、フラックスを求めるには、各点でvとSの単位面法線との内積をとればスカラー場となり、得られた場を上記と同様に積分すればよいことになる。すると、次の式が得られる。

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) )⋅ ( ∂ x ∂ s × ∂ t ) d s d t .￤int _{S}{Mathbf {v} }￤d{Mathbf {S} ￤d{Mathbf {S}=int _{S}({}mathbf {v} })\,dS=iint _{T}{mathbf {v} }(\mathbf {x} (s,t))\cdot ({}partial \mathbf {x} )\황황황황황황\over \partial t}right)ds\,dt.} $\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt.$

この式の右辺のクロスプロダクトはパラメトリゼーションによって決定される表面法線である。

この式は、左の積分を定義します（表面要素のドットとベクトル表記に注意してください）。

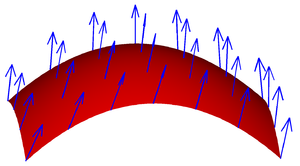
表面上のベクトル場。

表面積を含む定理

微分幾何学やベクトル計算を用いると、発散定理やその一般化であるストークスの定理など、表面積分に関する様々な有用な結果を導き出すことができる。

高度な課題

パラメータ設定の変更

上記の議論では、曲面 S のパラメトリゼーションを用いて曲面積分を定義しました。ある曲面はいくつかのパラメトリゼーションを持つことがあります。例えば、球面上で北極と南極の位置を移動させると、球面上のすべての点で緯度と経度が変化します。そこで、表面積分の定義が、どのようなパラメトリゼーションを選択したかに依存するかどうかが、自然な疑問となります。スカラー場の積分の場合、その答えは簡単で、どのようなパラメトリック化を用いても、表面積分の値は同じになります。

ベクトル場の積分は、表面法線が関係するため、より複雑です。数学者は、表面法線が同じ方向を向いている同じ表面の2つのパラメトリックがあると、両方のパラメトリックが表面積分に対して同じ値を与えることを証明しました。しかし、これらのパラメトリゼーションの法線が反対方向を向いている場合、一方のパラメトリゼーションを用いて得られる表面積分の値は、他方のパラメトリゼーションを用いて得られる値の負となります。つまり、曲面があれば、パラメトリゼーションにこだわる必要はないが、ベクトル場を積分するときには、法線がどの方向を向くかをあらかじめ決めておき、その方向と一致するパラメトリゼーションを選択する必要がある。

パラメタライゼーションはサーフェスの一部で機能する

もう一つの問題は、サーフェス全体をカバーするパラメトリケーションがない場合があるということです。その場合、表面をいくつかの部分に分割し、それぞれの部分の表面積分を計算し、それらをすべて足し合わせればよいということになります。しかし、ベクトル場を積分する場合、それぞれの曲面の法線ベクトルの選び方に注意しなければなりません。円柱の場合、側面の法線は本体の外側を指すと決めたら、上下の円形部分の法線も本体の外側を指すようにしなければならない、ということである。

サーフェス法線の非整合

最後に、各点で表面法線が整合しない曲面がある（例えば、メビウスの帯）。このような曲面を断片に分割し、それぞれの断片でパラメトリゼーションと対応する表面法線を選択し、断片を元に戻すと、異なる断片から来る法線ベクトルを調整することができません。これは、2つの断片の間のある接合部では、法線ベクトルが反対方向を向いていることを意味する。このような面を非配向性（non-orientable）と呼ぶ。ベクトル場は、非配向性の曲面では積分できない。